Елементи програмирања

Програмски језик је више од пуког средства за наређивање рачунару да изврши задатке. Језик такође служи и као окосница у којој програмери организују своје идеје о рачунским поступцима. Програми служе да пренесу те идеје међу члановима програмерске заједнице. Према томе, програми морају првенствено бити написани на начин да буду читљиви другим људима, а само успутно буду и извршавани на уређајима.

Приликом описа језика, потребно је посебно обратити пажњу на начине, то јест средства које језик пружа за комбиновање и спајање једноставних идеја да би се изградиле, односно образовале сложеније идеје. Сваки моћан програмски језик поседује три таква механизма:

• примитивне изразе и наредбе који представљају најједноставније структурне елементе које језик обезбеђује,

• средства комбиновања помоћу којих се сложени елементи граде из простијих, и

• начине апстракције којим се сложени елементи могу именовати и користити као јединични.

У програмирању постоје две врсте елемената: функције и подаци (иако ће ускоро бити разоткривено да и нису заиста толико различити). Неформално говорећи, подаци су ствари којима се жели манипулисати, а функције описују правила манипулисања подацима. Тако сваки моћан програмски језик треба да има могућност описа примитивних података и примитивних функција, као и да поседује неке методе комбиновања и апстраковања и једних и других, односно и функција и података.

Изрази

Након експериментисања с Пајтоновим интерпретатором у претходном одељку, сада ће изнова бити започет методички развој програмског језика Пајтон елемент по елемент. Треба бити стрпљив ако примери изгледају поједностављено јер узбудљивији материјал ускоро долази.

Отпочећемо примитивним изразима. Једна врста примитивног израза је број. Тачније, израз који је записан састоји се из цифара које представљају број у декадном систему.

>>> 42
42

Изрази који представљају бројеве могу се комбиновати и спајати с математичким операторима како би се образовали сложени изрази које ће интерпретатор вредновати:

>>> -1 - -1
0
>>> 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128
0.9921875

Ови математички изрази користе такозвани инфиксни запис у коме се оператор (на пример, +, -, * или /) појављује између операнада (бројева). Пајтон нуди много начина да се образују сложени изрази. Уместо пуког набрајања свих начина, биће постепено увођени нови облици израза заједно са језичким својствима које подржавају.

Позивни изрази

Најважнија врста сложених израза јесте израз позива или такозвани позивни израз који примењује функцију над неким аргументима. Присећајући се математичког појма функције из алгебре знамо да је то пресликавање неког улазног аргумента у излазну вредност. На пример, функција max пресликава своје улазе на један излаз који представља највећу вредност међу улазима. Начин на који Пајтон изражава примену функције исти је као и у математици.

>>> max(7.5, 9.5)
9.5

Овај позивни израз има и своје подизразе: оператор је израз који претходи заградама између којих се налази низ зарезом раздвојених израза који представљају операнде.

\[\underbrace{\quad\quad\quad\mathtt{max}\quad\quad\quad}_{\text{оператор}}(\underbrace{\quad\quad\quad\mathtt{7.5}\quad\quad\quad}_{\text{операнд}},\underbrace{\quad\quad\quad\mathtt{9.5}\quad\quad\quad}_{\text{операнд}})\]

Оператор специфицира функцију. Када се овај позивни израз вреднује каже се да је функција max позвана са или над аргументима 7.5 и 9.5, и враћа вредност 9.5.

Редослед аргумената у позивном изразу је од значаја. На пример, функција pow подиже свој први аргумент на степен представљен другим аргументом.

>>> pow(100, 2)
10000
>>> pow(2, 100)
1267650600228229401496703205376

Функционални запис има три главне предности у односу на математички конвенционалну инфиксну нотацију. Прво, функције могу примати произвољан број аргумената:

>>> max(1, -2, 3, -4)
3

Нема двосмислености пошто име функције увек претходи њеним аргументима.

Друго, функционална нотација се праволинијски може проширити на угнежђене изразе код којих су сами елементи сложени изрази. У угнежђеним позивним изразима, насупрот сложеним инфиксним изразима, структура угнежђивања је у потпуности одређена унутар заграда.

>>> max(min(1, -2), min(pow(3, 5), -4))
-2

Не постоји (принципијелно) ограничење дубине таквог угнежђивања ни свеукупне сложености израза коју Пајтонов интерпретатор може вредновати. Међутим, људи брзо постају збуњени вишеструким угнежђивањем. Важна улога програмера јесте да структуира изразе на такав начин да остану разумљиви како њему, тако и другим људима који ће можда читати његове изразе у будућности.

Треће, математички записи су врло разноврсни: множење се појављује између чиниоца, степеновање као експонент, дељење као разломачка црта, а квадратни корен као потпуно засебан симбол. Неке од ових записа није једноставно искуцати! Па ипак, сва ова сложеност се може ујединити кроз нотацију позивних израза. Иако Пајтон подржава уобичајене математичке операторе у инфиксној нотацији (као што су + и -), сваки оператор може бити изражен као именована функција.

Увоз библиотечких функција

Пајтон дефинише велики број функција, укључујући и претходно поменуте операторске функције, али нису сва њихова имена подразумевано на располагању. Уместо тога, функције и друге величине су разврстане по модулима који заједно чине Пајтонову библиотеку. За употребу ових елемената неопходно их је најпре увести. Примера ради, math модул обезбеђује разне познате математичке функције:

>>> from math import sqrt
>>> sqrt(256)
16.0

и operator модул пружа приступ функцијама које одговарају инфиксним операторима:

>>> from operator import add, sub, mul
>>> add(14, 28)
42
>>> sub(100, mul(7, add(8, 4)))
16

Наредба import одређује име модула (нпр. operator или math), а затим набраја имена атрибута из тог модула које треба увести (нпр. sqrt). Једном када се функција увезе, може бити позивана више пута.

Не постоји разлика између коришћења ових функцијских оператора (нпр. add) и симболичких оператора (нпр. +). Општеприхваћено је да већина програмера користи симболе и инфиксни запис да изразе једноставне аритметичке операције.

Документација Пајтон 3 библиотеке даје списак функција дефинисаних у сваком модулу, као на пример математички модул. Међутим, ова документација писана је за програмере који већ добро познају сам језик. За сада, експериментисање и играње са функцијама рећи ће више о понашању истих него читање документације. Како се временом буде напредовало и упознавало с Пајтон програмским језиком и речником заједнице, ова документација ће постати драгоцен референтни извор.

Имена и окружење

Критичан аспект програмског језика јесу начини и средства које пружа за обраћање рачунским објектима кроз коришћење имена. Уколико се вредности додели име, каже се да је то име везано за или на ту вредност.

У Пајтону, могуће је успоставити нове везе користећи се наредбом доделе која садржи име с леве стране знака = и вредност с десне стране:

>>> полупречник = 10
>>> полупречник
10
>>> 2 * полупречник
20

Имена се такође повезују и преко import наредбе.

>>> from math import pi
>>> pi * 71 / 223
1.0002380197528042

Знак = се назива оператор доделе у Пајтону (и у многим другим програмским језицима). Додела је најпростије средство апстракције које дозвољава коришћење једноставних имена којима се обраћа на резултате сложених операција, као што је обим или површина круга израчуната у наставку. Овим путем, сложени програми се граде поступно, корак по корак, спајањем рачунских објеката све веће сложености.

Могућност везивања имена на вредности као и потоње поновно добијање тих вредности преко имена подразумева да интерпретатор мора садржати и неку врсту меморије која прати имена, вредности, и везе. Ова меморија назива се окружење.

Имена се такође везују и на функције. Примера ради, име max је везано на функцију за проналажење максимума која је малочас коришћена. Функције, насупрот бројевима, је теже приказати као текст, па Пајтон уместо тога исписује идентификациони опис приликом упита да опише функцију:

>>> max
<built-in function max>

Може се користити наредба доделе да се дају нова имена постојећим функцијама.

>>> f = max
>>> f
<built-in function max>
>>> f(2, 3, 4)
4

Узастопне наредбе доделе могу превезати одређено име на нову вредност.

>>> f = 2
>>> f
2

У Пајтону се имена често називају и имена променљивих или просто променљиве због тога што могу бити повезана на различите вредности током извршења програма. Када се име повеже на нову вредност путем доделе, више није везано ни за једну претходну вредност. Чак се и уграђена имена могу повезати на нове вредности.

>>> max = 5
>>> max
5

Након доделе вредности 5 имену max, назив max више није повезан на функцију те ће покушај позива max(2, 3, 4) проузроковати грешку.

Приликом извршавања наредбе доделе Пајтон вреднује израз с десне стране знака = пре промене везе на име с леве стране. Стога се може позивати на име и у изразу с десне стране чак и ако је то име предвиђено за повезивање кроз наредбу доделе.

>>> x = 2
>>> x = x + 1
>>> x
3

Такође је могуће повезати више имена на више вредности унутар једне наредбе у којој су имена с леве стране знака = и изрази с десне стране знака = раздвојени зарезима.

>>> обим, површина = 2 * pi * полупречник, pi * полупречник * полупречник
>>> обим
62.83185307179586
>>> површина
314.1592653589793

Смена вредности једне променљиве не утиче на друга имена. Иако је променљива површина у наставку повезана на вредност изворно дефинисану преко назива полупречник, вредност везана на име површина није промењена. Ажурирање вредности везане на име површина захтева још једну наредбу доделе.

>>> полупречник = 11
>>> површина
314.1592653589793
>>> површина = pi * полупречник * полупречник
>>> површина
380.1327110843649

Код вишеструких додела, сви изрази с десне стране знака = бивају вредновани пре било ког повезивања имена с леве стране на те вредности. Као резултат овог правила, замена вредности повезаних на два имена може се извести у једној наредби.

>>> x, y = 3, 4.5
>>> y, x = x, y
>>> x
4.5
>>> y
3

Вредновање угнежђених израза

Један од циљева овог поглавља јесте да се одговори на питања и отклоне потенцијални проблеми у процедуралном начину размишљања. Као један од репрезентативних случајева биће размотрено вредновање угнежђених позивних израза. Сам интерпретатор прати поступак.

Да би вредновао позивни израз, Пајтон ће урадити следеће:

1. Вредновати подизразе оператора и операнада, а затим

2. Применити функцију која је вредност операторског подизраза на аргументе који су вредности подизраза операнада.

Чак и један овакав једноставан поступак илуструје неке важне ставке о процесима уопште. Први корак диктира то да би се спровео поступак вредновања позивног израза неопходно је најпре вредновати остале изразе. Према томе, поступак вредновања је природно рекурзиван, односно, као један од корака укључује неопходност да се позове на сопствена правила.

На пример, вредновање

>>> sub(pow(2, add(1, 10)), pow(2, 4))
2032

захтева да се претходно описани поступак вредновања примени четири пута. Уколико би се нацртао сваки израз који се вреднује, могуће је графички приказати хијерархијску структуру овог поступка.

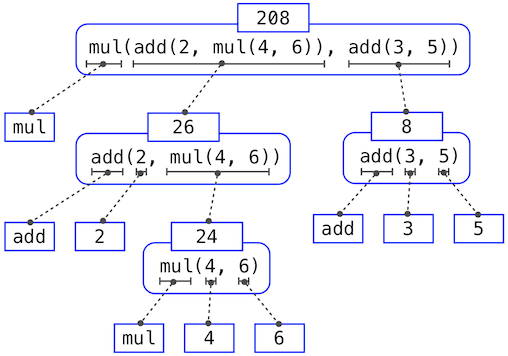
Ова илустрација се назива стабло израза. У рачунарству, стабла по правилу расту одозго према доле. Објекти у свакој тачки стабла називају се чворови и у овом конкретном случају чворови су изрази упарени са својим вредностима.

Вредновање корена стабла, односно целокупног израза на врху, захтева најпре вредновање грана које су заправо његови подизрази. Изрази у листовима (то јест, чворовима без грана које произилазе из њих) представљају или функције или бројеве. Унутрашњи чворови имају два дела: позивни израз на који се правило вредновања примењује, као и резултат тог израза. Гледајући на вредновање у смислу оваквог стабла, може се замислити да вредности операнада израњају нагоре полазећи од завршних, односно крајњих чворова и укрштајући се на вишим и вишим нивоима.

Даље, треба имати на уму да поновне примене првог корака доводе до тачке где је потребно вредновати не више позивне изразе, већ примитивне изразе као што су бројеви (нпр. 2) и имена (нпр. add). Примитивни случајеви се обрађују према правилу који гласи:

• цифра се вреднује у број који означава,

• име се вреднује у вредност придружену том имену у тренутном окружењу.

Треба запазити важну улогу коју има окружење у одређивању значења симбола у изразима. Бесмислено је у Пајтону говорити о вредности израза као што је

>>> add(x, 1) 

без навођења било каквих информација о окружењу које би пружиле смисао имену x (па чак и имену add). Окружења обезбеђују контекст у коме се вредновање израза одвија, а који игра важну улогу у разумевању начина на који се програми извршавају.

Наведени поступак вредновања није довољан да би се вредновао целокупан Пајтонов изворни код већ само позивне изразе, бројеве и имена. На пример, не обрађује наредбе доделе. Извршавање

>>> x = 3

не враћа вредност нити вреднује функцију на неким аргументима пошто је уместо тога сврха доделе да повеже име на вредност. Углавном, наредбе се не вреднују него се извршавају. Оне не производе вредност већ чине неку промену. Свака врста израза или наредбе има свој поступак вредновања или извршавања.

Опаска за педантне: када се каже „цифра се вреднује у број”, мисли се заправо на то да Пајтонов интерпретатор вреднује цифру у број. Интерпретатор је тај који даје значење програмском језику. С обзиром на то да је интерпретатор постојан програм који се увек понаша доследно, може се рећи да се цифре (и изрази) саме по себи вреднују у вредности у контексту Пајтон програма.

Нечиста print функција

Кроз читав овај текст, биће разликоване две врсте функција, чисте и нечисте.

Чисте функције

Чисте функције имају неки улаз (односно своје аргументе) и враћају неки излаз (резултат њихове примене). Уграђена функција

>>> abs(-2)
2

се може приказати као мала машина која узима улаз и производи излаз.

Функција abs је чиста. Чисте функције имају својство да њихова примена нема других ефеката осим враћања вредности. Штавише, чисте функције морају увек враћати исту вредност када су позване са истим аргументима.

Нечисте функције

Поред тога што враћа вредност, примена нечисте функције изазива и такозване бочне ефекте који праве неке промене у стању интерпретатора или рачунара. Чест бочни ефекат јесте производња додатног излаза поред повратне вредности користећи се print функцијом.

>>> print(1, 2, 3)
1 2 3

Иако print и abs могу изгледати слично у овим примерима, ипак функционишу на суштински различите начине. Вредност коју print враћа је увек None, што је посебна Пајтон вредност која представља ништа. Интерактивни Пајтон интерпретатор не исписује аутоматски вредност None. У случају функције print, сама функција исписује излаз као бочни ефекат позива.

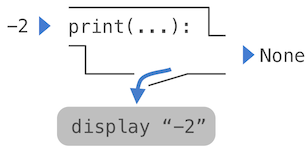
Угнежђени изрази позива print функције истичу њену нечисту природу.

>>> print(print(1), print(2))
1
2
None None

Уколико се претходни резултат на први поглед учини неочекиваним, увек се може нацртати стабло израза како би се разјаснило зашто вредновање оваквих израза производи наизглед чудне излазе.

Треба бити обазрив са print функцијом! Чињеница да print функцијом враћа None значи да никада не би требала да буде део израза у наредби доделе.

>>> два = print(2)
2
>>> print(два)
None

Чисте функције су ограничене по томе што не могу да имају бочне ефекте или да мењају понашање с временом. Наметање ових ограничења доноси значајне користи. Прво, чисте функције се могу поузданије комбиновати и слагати у сложене позивне изразе. У претходном примеру нечисте функције може се видети да print не враћа користан резултат када се користи као израз за операнд. С друге стране, показано је да се функције као што су max, pow или sqrt могу ефикасно користити у угнежђеним изразима.

Друго, чисте функције су обично једноставније за тестирање. Низ аргумената ће увек водити ка истим повратним вредностима које се могу поредити са очекиваним повратним вредностима. Тестирање ће бити разматрано детаљније нешто касније у овом поглављу.

Треће, последње поглавље приказује да су чисте функције есенцијалне у писању конкурентних програма у којима се вишеструки позивни изрази вреднују истовремено.

За разлику од тога, следеће поглавље истражује читаву плејаду нечистих функција и описује њихову употребу.

Из ових разлога, у наставку текућег поглавља јак акценат ће бити стављен на писање и коришћење чистих функција. Функција print је изузетак који је коришћен само како би били приказани међурезултати израчунавања.