Рекурзивне функције

Функција је рекурзивна ако унутар тела функције позива саму себе било директно или индиректно. Другим речима, ток извршења тела рекурзивне функције може захтевати позив те функције поново. Рекурзивне функције у Пајтону не користе никакву посебну синтаксу, али захтевају известан напор да се разумеју и напишу.

Почећемо примером задатка: написати функцију која сабира цифре природног броја. Приликом пројектовања рекурзивне функције траже се начини да се проблем растави на једноставније потпроблеме. У овом конкретном случају, оператори % и // се могу користити да се број раздвоји на два дела: цифру најмање тежине и остатак броја.

>>> 18117 % 10
7
>>> 18117 // 10
1811

Збир цифара броја 18117 је \(1+8+1+1+7=18\). Баш као што је могуће раздвојити број, може се раздвојити и овај збир на последњу цифру, 7, и збир свих цифара изузев последње, \(1+8+1+1=11\). Ово раздвајање даје алгоритам: да се саберу цифре броја n, додати његову последњу цифру n % 10 на збир цифара броја n // 10. Постоји један посебан случај: ако је број једноцифрен, тада је збир његових цифара управо сам тај број. Овај алгоритам може се имплементирати као рекурзивна функција.

>>> def збирЦифара(n):
...     """Враћа збир цифара природног броја n."""
...     if n < 10:
...         return n
...     else:
...         свеСемПоследњеЦифре, последњаЦифра = n // 10, n % 10
...         return збирЦифара(свеСемПоследњеЦифре) + последњаЦифра

Оваква дефиниција збирЦифара је истовремено и потпуна и исправна упркос томе што је функција збирЦифара позвана унутар сопственог тела. Задатак израчунавања збира цифара броја је подељен на два корака: збир свих цифара изузев последње и додавања последње цифре. Оба ова корака су једноставнија од почетног задатка. Функција је рекурзивна зато што је први корак заправо исти тип задатка као и оригинални задатак. То јест, збирЦифара је функција која је потребна да би се имплементирао збирЦифара.

>>> збирЦифара(9)
9
>>> збирЦифара(18117)
18
>>> збирЦифара(9437184)
36
>>> збирЦифара(11408855402054064613470328848384)
126

Могуће је тачно разумети како ова рекурзивна функција бива позивана користећи окружење модела израчунавања. Нису неопходна никаква додатна нова правила.

Када се def наредба изврши, назив збирЦифара је повезан на новостворену функцију, али тело те функције још увек није извршено. Због тога, кружна природа функције збирЦифара још увек не представља проблем. Затим се збирЦифара позива над аргументом 738, рецимо:

1. Ствара се локални оквир за збирЦифара у коме је n повезано на 738 и тело функције збирЦифара се извршава у окружењу које започиње тим оквиром.

2. Како 738 није мање од 10, наредба доделе вредности се извршава делећи број 738 на 73 и 8.

3. У return наредби која следи, збирЦифара се позива над аргументом 73, што је вредност променљиве свеСемПоследњеЦифре у тренутном окружењу.

4. Други локални оквир за збирЦифара је створен, али овога пута са n увезаним на 73. Тело функције збирЦифара се поново извршава, сада у новом окружењу које почиње овим оквиром.

5. Пошто 73 такође није мање од 10, број 73 се дели на 7 и 3 и збирЦифара бива позван над 7 што је вредност променљиве свеСемПоследњеЦифре вредноване у овом оквиру.

6. Трећи локални оквир за функцију збирЦифара је створен са n повезаним на 7.

7. У окружењу које започиње овим оквиром провера n < 10 је тачна те је зато 7 повратна вредност.

8. У другом локалном оквиру, ова враћена вредност 7 се сабира са 3, што је вредност променљиве последњаЦифра, да би се вратила вредност 10.

9. У првом локалном оквиру, ова враћена вредност 10 се сабира са 8, што је вредност променљиве последњаЦифра, да би се вратила вредност 18.

Упркос својој кружној одлици, ова рекурзивна функција примењује се исправно зато што бива примењена два пута, али с различитим аргументима. Штавише, други позив функције био је једноставни случај почетног задатка да се израчуна збир цифара броја. При позиву функције збирЦифара над произвољно великим аргументом, може се једноставним скицирањем окружења показати да сваки наредни позив функције збирЦифара узима мањи аргумент од претходног, све док се најзад не дође до једноцифреног улаза.

Овај пример такође илуструје како се функције које имају једноставна тела могу развити у сложене процесе израчунавања користећи рекурзију.

Анатомија рекурзивних функција

У телу многих рекурзивних функција проналази се заједнички шаблон. Тело започиње основним случајем, условном наредбом која дефинише понашање функције за тривијалне улазе, односно аргументе најједноставније за обраду. У примеру збирЦифара, основни случај је сваки једноцифрен аргумент који уједно представља и повратну вредност. Поједине рекурзивне функције ће имати више основних случајева.

Основни случајеви су праћени од стране једног или више рекурзивних позива. Рекурзивни позиви увек упрошћавају почетни проблем. Рекурзивне функције изражавају израчунавање кроз постепено поједностављивање проблема. На пример, сабирање цифара броја 7 је једноставније од сабирање цифара броја 73, што је опет једноставније од сабирања цифара броја 738. За сваки следећи позив функције, преостало је мање посла да се обави.

Рекурзивне функције често решавају проблеме на другачији начин од итеративних приступа који су коришћени раније. Размотрити функцију факт која израчунава факторијел од n, где примера ради факт(4) рачуна \(4!=4\cdot3\cdot2\cdot1=24\).

Природна имплементација коришћењем while наредбе акумулира производ множећи све природне бројеве до n.

>>> def фактИтер(n):
...     производ, k = 1, 1
...     while k <= n:
...        производ, k = производ * k, k + 1
...     return производ
>>> фактИтер(4)
24

С друге стране, рекурзивна имплементација факторијела може изразити факт(n) преко факт(n-1), што је једноставнији проблем. Основни рекурзивни случај је најједноставнији облик проблема, односно: факт(1) је 1.

Претходне две факторијел фукнције се концептуално разликују. Итеративна функција постепено гради резултат почевши од основног случаја за 1 све до коначног производа кроз узастопна множења сваког чиниоца. Рекурзивна функција, у другу руку, гради резултат директно од последњег чиниоца, n, и резултата једноставнијег проблема, факт(n-1).

Како се рекурзија „одмотава” кроз сукцесивне примене факт фукције на све једноставније и једноставније инстанце проблема, резултат најзад бива изграђен почевши од основног случаја. Рекурзија се завршава прослеђивањем аргумента 1 функцији факт. Резултат сваког позива зависи од наредног све док се не стигне до основног случаја.

Исправност ове рекурзивне фукнције је лако потврдити преко стандардне дефиниције математичке функције факторијел:

\[\begin{split}(n-1)!&=(n-1)\cdot(n-2)\cdot\cdots\cdot3\cdot2\cdot1\\ n!&=n\cdot(n-1)\cdot(n-2)\cdot\cdots\cdot3\cdot2\cdot1\\ n!&=n\cdot(n-1)!\end{split}\]

Иако је могуће размотати рекурзију користећи постојећи модел израчунавања, често је јасније размишљати о рекурзивним позивима као функционалним апстракцијама. То јест, не треба бринути о томе како је факт(n-1) имплементирано у телу функције факт, већ једноставно веровати да рачуна факторијел аргумента n-1. Третирање рекурзивних позива као функционалне апстракције је назван рекурзивни скок вере. Функција се дефинише преко саме себе и приликом провере исправности функције просто се верује, односно претпоставља да једноставнији случај ради исправно. У овом примеру верује се да факт(n-1) тачно рачуна \((n-1)!\) па се стога само проверава да је \(n!\) исправно израчунато под условом да је претходна претпоставка тачна. На овај начин, провера исправности рекурзивне функције је облик индуктивног доказа.

Функције фактИтер и факт се такође разликују зато што се у првопоменутој имплементацији морају увести две додатне променљиве, производ и k које нису неопходне у рекурзивној имплементацији. Итеративне функције углавном морају успоставити и одржавати нека локална стања која се мењају током читавог рачунања. У сваком тренутку, то стање карактерише резултат обављеног посла као и преосталу количину посла. На пример, када је k једнако 3, а производ једнак 2, преостају још два члана да се обраде, 3 и 4. С друге стране, факт функција је одређена једним аргументом n. Стање израчунавања је у потпуности садржано унутар структуре окружења, тачније кроз повратне вредности које имају улогу производа и повезују n на различите вредности у различитим оквирима уместо да експлицитно прате k.

Рекурзивне функције користе правила вредновања позивних израза да повежу имена на вредности притом често избегавајући сметње проузроковане доделама локалних имена унутар итерације. Из овог разлога рекурзивне функције се лакше дефинишу на исправан начин. Међутим, учење да се препознају процеси израчунавања развијени из рекурзивних функције свакако захтевају вежбу.

Међусобна рекурзија

Када је рекурзивна процедура подељена између две функције које позивају једна другу, каже се да су функције међусобно рекурзивне. Као пример размотрити следећу дефиницију парности и непарности за природне бројеве:

• број је паран ако је за један већи од непарног броја;

• број је непаран ако је за један већи од парног броја;

• нула је парна.

Користећи ову дефиницију, могуће је имплементирати међусобно рекурзивне функције које одређују да ли је број паран или непаран:

Међусобно рекурзивне функције могу се претворити у појединачно рекурзивне функције кроз пробијање границе апстракције између две функције. У овом примеру, тело функције јеНепаран може се припојити телу функције јеПаран водећи рачуна да се n унутар тела функције јеНепаран замени са n-1 како би одразио прослеђени јој аргумент:

>>> def јеПаран(n):
...     if n == 0:
...         return True
...     else:
...         if (n-1) == 0:
...             return False
...         else:
...             return јеПаран((n-1)-1)

Као таква, међусобна рекурзија није ништа тајанственија нити моћнија од једноставне рекурзије, али пружа механизам одржавања апстракције унутар компликованих рекурзивних програма.

Испис унутар рекурзивних функција

Рачунски процес развијен кроз рекурзивну функцију често се може осликати користећи print позиве. Као пример, биће иплементирана функција каскада која исписује све префиксе неког броја од најдужег ка најмањем и натраг до најдужег.

>>> def каскада(n):
...     """Исписује каскаду префикса броја n."""
...     if n < 10:
...         print(n)
...     else:
...         print(n)
...         каскада(n//10)
...         print(n)

>>> каскада(2023)
2023
202
20
2
20
202
2023

У овој рекурзивној функцији, основни случај јесте једноцифрени број, који се исписује. Иначе, рекурзивни позив је постављен између два print позива.

Није строг услов да се основни случај изрази пре рекурзивних позива. Заправо, ова функција се може компактније изразити уз опаску да се print(n) понавља у оба случаја условне наредбе те јој стога може претходити.

>>> def каскада(n):
...     """Исписује каскаду префикса броја n."""
...     print(n)
...     if n >= 10:
...         каскада(n//10)
...         print(n)

Као други пример међусобне рекурзије, размотрити игру у којој се на почетку на столу налази \(n\) облутака. Два играча у сваком кругу узимају по један или два облутка са стола. Победник је онај играч који узме последњи облутак. Претпоставити да играчи А и Б играју ову игру, сваки од њих користећи просту стратегију:

• Играч А увек узима по један облутак;

• Играч Б узима два облутка ако је на столу паран број облутака, а иначе један.

Уколико је дато \(n\) облутака и ирач А започиње игру, ко ће победити?

Природно растављање овог задатка јесте кроз раздвајање сваке од стратегија у засебну функцију. Ово дозвољава потенцијалну промену сваке од стратегија без утицаја на ону другу тако одржавајући апстрактну преграду између њих. Да би се укључила кружна природа игре, ове две функције позивају једна другу на крају сваког круга.

>>> def играчА(n):
...     if n == 0:
...         print("Играч Б побеђује!")
...     else:
...         играчБ(n-1)

>>> def играчБ(n):
...     if n == 0:
...         print("Играч А побеђује!")
...     elif јеПаран(n):
...         играчА(n-2)
...     else:
...         играчА(n-1)

>>> играчА(20)
Играч Б побеђује!

Унутар тела функције играчБ примећују се вишеструки рекурзивни позиви. Међутим, у овом случају, сваки позив функције играчБ позива функцију играчА највише једном. У следећем одељку биће размотрено шта се дешава када један позив функције прави вишеструке директне рекурзивне позиве.

Стабло рекурзије

Још један уобичајени образац израчунавања јесте такозвано стабло рекурзије где функција позива саму себе више од једном. Као пример размотрити израчунавање низа Фибоначијевих бројева у ком сваки члан представља збир претходна два.

У поређењу са претходним покушајима, ова рекурзивна дефиниција је јако привлачна јер тачно одражава опште познату дефиницију Фибоначијевих бројева. Размотрити образац израчунавања који је резултат извршавања функције фиб(6), приказан у наставку. Да би се израчунао фиб(6), израчунавају се најпре фиб(5) и фиб(4). Да би се израчунао фиб(5), израчунавају се фиб(4) и фиб(3). Генерално гледано, овај поступак израчунавања изгледа попут стабла (дијаграм у наставку није потпуни дијаграм окружења, већ поједностављени приказ поступка израчунавања). Свака плава тачка означава завршено израчунавање Фибоначијевог броја у процесу проласка кроз ово стабло.

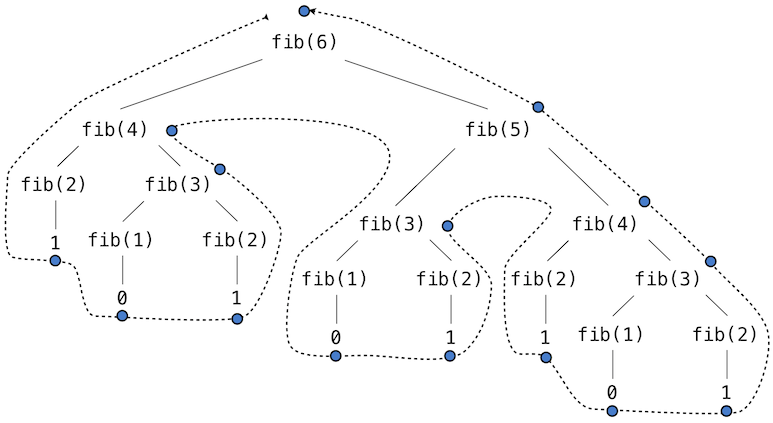
За функцију са вишеструким рекурзивним позивима се каже да представља стабло рекурзије због тога што се сваки позив грана на више мањих позива од који се сваки даље рачва у још мање позиве, баш као што и гране дрвета постају мање и бројније како се шире од стабла. Ова функција је поучна као прототипска рекурзија стабла, али је ужасно неефикасан начин за одређивање Фибоначијевог низа јер врши толико сувишних израчунавања. Треба приметити да је целокупно израчунавање фиб(4), што је готово половина посла, дуплирано. У ствари, није тешко показати да ће функција израчунати фиб(1) или фиб(2) (што представља број листова у стаблу) тачно фиб(n+1) пута. Да би се уопште схватило до које мере је ово лоше и неефикасно, лако се може показати да вредност фиб(n) расте експоненцијално са порастом n. Рецимо, фиб(40) је 63’245’986! Горња функција извршава кораке чији број расте експоненцијално са улазом.

Већ је показано да је могуће дефинисати функцију која израчунава Фибоначијеве бројеве без стабла рекурзије. Заправо, претходни покушаји су били далеко ефикаснији, што је тема која ће бити разматрана нешто касније. Претходно приказана итеративна имплементација Фибоначијевих бројева, поновљена је овде ради боље прегледности.

>>> def фибИтеративно(n):
...     """Израчунава n-ти Фибоначијев број, за n >= 2."""
...     претходни, тренутни = 0, 1   # први и други Фибоначијев број
...     k = 2                        # тренутни Фибоначијев број
...     while k < n:
...         претходни, тренутни = тренутни, претходни + тренутни
...         k = k + 1
...     return тренутни

Стање које се у овом случају мора одржавати састоји се од тренутног и претходног Фибоначијевог броја, заједно са индексом тренутног броја. Ова дефиниција не одражава стандардну математичку дефиницију Фибоначијевих бројева тако јасно као рекурзивни приступ. Међутим, количина израчунавања потребна у итеративној имплементацији само је линеарна у односу на n, а не експоненцијална. Чак и за мале вредности n, ова разлика може бити огромна.

Из ове разлике не треба закључити да су поступци који укључују стабла рекурзије бескорисни. Када се узму у обзир поступци који оперишу над хијерархијски структурираним подацима, а не бројевима, биће откривено да су стабла рекурзије врло природно и моћно средство. Осим тога, поступци који укључују стабла рекурзије често се могу учинити далеко ефикаснији, као што ће бити приказано у трећем поглављу.

У наставку ће бити приказан проблем за који је решење преко стабла рекурзије знатно једноставније од било које итеративне алтернативе.

Пример: Партиције

Број партиција природног броја \(n\), користећи се сабирцима мањим или једнаким од \(m\), је број начина на који се број \(n\) може изразити као збир природних бројева не већих од \(m\) у неопадајућем редоследу. На пример, број партиција броја 6, користећи се деловима не већим од 4 јесте девет.

1. \(6 = 2 + 4\)

2. \(6 = 1 + 1 + 4\)

3. \(6 = 3 + 3\)

4. \(6 = 1 + 2 + 3\)

5. \(6 = 1 + 1 + 1 + 3\)

6. \(6 = 2 + 2 + 2\)

7. \(6 = 1 + 1 + 2 + 2\)

8. \(6 = 1 + 1 + 1 + 1 + 2\)

9. \(6 = 1 + 1 + 1 + 1 + 1 + 1\)

Биће дефинисана функција бројПартиција(n, m) која враћа број различитих партиција аргумента n користећи делове мање или једнаке од m. Ова функција има једноставно решење користећи се стаблом рекурзије које је засновано на следећем запажању:

Број начина на који се може партиционисати \(n\) користећи бројеве не веће од \(m\) једнак је:

1. броју начина да се партиционише \(n-m\) користећи делове мање или једнаке од \(m\), и

2. броју начина да се партиционише \(n\) користећи делове не веће од \(m-1\).

Да би се схватило зашто је претходно тврђење тачно, треба уочити да се укупан број начина за партиционисање \(n\) може поделити у два дисјунктна подскупа: први који садржи макар једно \(m\) и други који не садржи ниједно. Штавише, свако партиционисање из првог подскупа јесте заправо партиција броја \(n-m\) праћена \(m\) као последњим сабирком. У горњем примеру, прве две партиције садрже 4, док осталих седам не садржи.

Стога, могуће је рекурзивно упростити проблем партиционисања \(n\) користећи бројеве мање или једнаке \(m\) на два једноставнија потпроблема: (1) партиционисање мањег броја \(n-m\), и (2) партиционисање са мањим саставним деловима не већим од \(m-1\).

Да би се довршила имплементација, неопходно је назначити и следеће основне случајеве:

1. Постоји један начин да се партиционише 0 који не садржи ниједан сабирак.

2. Постоји нула начина да се партиционишу негативни бројеви.

3. Не постоји начин да се природан број партиционише непозитивним бројевима.

   >>> def бројПартиција(n, m):
   ...     """Враћа број партиција броја n користећи сабирке не веће од m."""
   ...     if n == 0:
   ...         return 1
   ...     elif n < 0:
   ...         return 0
   ...     elif m == 0:
   ...         return 0
   ...     else:
   ...         return бројПартиција(n-m, m) + бројПартиција(n, m-1)
   

   >>> бројПартиција(6, 4)
   9
   >>> бројПартиција(5, 5)
   7
   >>> бројПартиција(10, 10)
   42
   >>> бројПартиција(15, 15)
   176
   >>> бројПартиција(20, 20)
   627
   

Може се размишљати о стаблима рекурзије као о истраживању различитих могућности. У овом конкретном случају, истражује се могућност да се користе делови величине \(m\) и могућност да се не користе. Први и други рекурзивни позив управо одговарају овим могућностима.

Имплементација ове функције без рекурзије била би знатно запетљанија. Заинтересовани читаоци се охрабрују да покушају.

Пример: Враћање кусура

Размотримо следеће хипотетичко питање: да ли сте се икада запитали на колико различитих начина у продавници можете добити кусур у висини одређеног износа користећи кованице од 1, 2, 5, 10 и 20 динара? Односно још уопштеније, може ли се написати функција за израчунавање броја начина за враћање било које унапред задате новчане вредности?

Овај проблем има једноставно решење у виду рекурзивне функције. Претпоставимо да вредности новчића, тј. кованица, имамо распоређене по неком редоследу (рецимо од виших ка нижим). Тада важи следећа релација:

Број начина за враћање кусура \(k\) користећи \(n\) врста кованица једнак је:

• број начина за враћање кусура \(k\) користећи све кованице изузев прве, плус

• број начина за враћање кусура \(k-d\) коришћењем свих \(n\) врста кованица, где је \(d\) вредност прве кованице.

Да би се увидело зашто претходна тврдња важи, треба запазити да се начини враћања кусура могу поделити у два скупа: они који не користе ниједан новчић прве вредности и они које то чине. Према томе, укупан број начина за враћање одређеног износа кусура једнак је броју начина за враћање износа кусура без употребе прве кованице из низа, плус број начина за враћање под претпоставком да се користи први новчић. Међутим, овај последњи број једнак је броју начина за враћање износа кусура који преостаје након употребе прве кованице у низу.

Дакле, може се рекурзивно смањити проблем враћања задатог износа кусура на проблем враћања мањих износа користећи мањи број кованица. Треба пажљиво размислити и размотрити претходно правило смањења и прихватити да се оно може искористити за описивање алгоритма ако се наведу и следећи специјални случајеви:

• Ако је \(k\) тачно 0, то би се требало рачунати као један начин за враћање кусура.

• Ако је \(k\) мање од 0, то би се требало рачунати као 0 начина за враћање кусура.

• Ако је \(n\) једнако 0, то би се такође требало рачунати као 0 начина за враћање кусура.

Овај опис може се лако превести у рекурзиван поступак:

>>> def кусур(износ, апоени):
...     """ износ:  произвољан природан броj;
...         апоени: низ или поворка природних броjева;
...         враћа:  броj начина да се врати износ користећи апоене."""
...     if износ == 0:
...         return 1
...     if износ < 0 or len(апоени) == 0:
...         return 0
...     return кусур(износ - апоени[0], апоени) + кусур(износ, апоени[1:])

Сада се може претходна функција употребити да се одговори на питање на колико начина је могуће кованицама вратити кусур од 100 динара:

>>> кусур(100, [1, 2, 5, 10, 20])
4111

Функција кусур генерише стабло рекурзије са редундансама сличним онима у првој имплементацији фиб функције. (Требаће доста времена да се израчуна 4111 начина.) С друге стране, није очигледно како испројектовати бољи и ефикаснији алгоритам за израчунавање резултата, а овај проблем оставља се као изазов читаоцу. Запажање да рекурзивни поступак може бити крајње неефикасан, иако га је често лако описати и разумети, навело је људе да предложе идеју о преузимању најбољих ствари из оба света пројектовањем такозваног „паметног преводиоца” који би трансформисао стабла рекурзија у ефикасније поступке израчунавања којима би се долазило до истог резултата.

Један приступ у савладавању редундантних и сувишних израчунавања је сређивање ствари тако да се у току израчунавања аутоматски прави и попуњава табела вредности. Сваки пут када се позове функција над неким аргументом најпре се погледа да ли је вредност већ сачувана у табели, у ком случају се избегава излишно израчунавање. Ова стратегија, позната као табулација или мемоизација, може се имплементирати праволинијски. Табулација се понекад може користити за трансформисање поступака који захтевају експоненцијални број корака (као што је кусур) у поступке чији захтеви за простором и временом расту линеарно са порастом улаза. Више речи о мемоизацији биће у одељку о ефикасности у оквиру наредног поглавља.