Променљиви подаци¶
Видели смо колико је апстракција битна као помоћно средство у борби са сложеношћу великих система. Ефикасно програмирање такође захтева организационе принципе који воде ка формулисању целокупног пројекта програма. Конкретно, потребне су стратегије које ће помоћи приликом устројства великих система како би били модуларни, што значи да се природно деле на кохерентне делове који се могу засебно развијати и одржавати.
Једна моћна техника за стварање модуларних програма је уметање података чије се стање временом може мењати. На овај начин, један објекат података може представљати нешто што се развија независно од остатка програма. На понашање променљивог објекта може утицати његова историја, баш као што утиче и на бића у стварном свету. Додавање стања подацима је централни састојак парадигме која се назива објектно-оријентисано програмирање.
Метафора објекта¶
На почетку овог текста, направљена је разлика између функција и података: функције су вршиле операције, а над подацима је оперисано. Када су у податке увршћене и вредности функција, то је имплицитно значило признање да подаци такође могу имати понашање. Функцијама се може малипулисати као подацима, али се такође могу позивати за обављање израчунавања.
Објекти спајају вредности података с понашањем. Објекти представљају информације, али се такође понашају попут ствари које приказују. Логика начина на који објекти узајамно дејствују и комуницирају са другим објектима је запакована заједно са информацијама које кодирају вредност објекта. Када се објекат испише, он зна како то треба учинити. Уколико је објекат састављен из делова, зна како те делове да открије и прикаже када му се упути такав захтев. Објекти су истовремено и информације и поступци, сједињени заједно како би представили својства, интеракције и понашања сложених ствари.
Понашање објеката је имплементирано у Пајтону кроз посебну објектну синтаксу и придружену терминологију која ће бити уведена примером. Датум је врста објекта.
>>> from datetime import date
Назив date је везан за класу. Као што је виђено, класа представља неку врсту вредности. Појединачни датуми називају се инстанцама те класе. Инстанце се могу створити позивањем класе над аргументима који одликују ту инстанцу.
>>> небоСеОтворило = date(1991, 5, 29)
Иако је небоСеОтворило направљено од примитивних бројева, ипак се понаша као датум. На пример, одузимање од другог датума даће временску разлику која се може исписати.
>>> print(date(1991, 12, 8) - небоСеОтворило)
193 days, 0:00:00
Објекти имају атрибуте, што су заправо именоване вредности које су део тог објекта. У Пајтону, као и у многим другим програмским језицима, користи се тачка, то јест тачкаста нотација како би се означио атрибут објекта.
<израз> . <име>
Изнад, <израз> се вреднује у објекат, а <име> је име атрибута тог објекта.
За разлику од имена која су до сада разматрана, ова имена атрибута нису доступна у општем окружењу. Уместо тога, имена атрибута су посебна за инстанцу објекта која претходи тачки.
>>> небоСеОтворило.year
1991
Објекти такође имају методе, а нису ништа друго до атрибути са функцијама као вредностима. Метафорично, каже се да објекат „зна” како да спроведе те методе. Гледано кроз имплементацију, методе су функције које израчунавају своје резултате на основу својих аргумената и свог објекта. На пример, strftime метода (класичан назив функције који претвара и форматира време у ниску) инстанце небоСеОтворило прима један аргумент који специфицира како приказати датум (нпр. %A значи да би требало у целости исписати дан у недељи).
>>> небоСеОтворило.strftime('%A, %B %d')
'Wednesday, May 29'
Израчунавање повратне вредности strftime захтева два улаза: ниску која описује формат излаза и информације о датуму која је запакована у небоСеОтворило. Логика која се посебно односи на датум примењује се у оквиру ове методе како би се добио претходни резултат. Никада није речено да је 29. мај 1991. године била среда, али знање одговарајућег дана у недељи је део онога што датум представља. Спајањем понашања и информација заједно, овај Пајтон објекат нуди убедљиву и самосталну апстракцију датума.
Датуми су објекти, али и бројеви, ниске, низови и распони су такође све објекти. Они представљају вредности, али се уједно и понашају на начин који одговара вредностима које представљају. Они такође имају своје атрибуте и методе. Примера ради, ниске имају низ метода које олакшавају обраду текста.
>>> '1234'.isnumeric()
True
>>> 'вЛАДИМИР мИЛОВАНОВИЋ'.swapcase()
'Владимир Миловановић'
>>> 'Влада'.upper().endswith('ДА')
True
Заправо, све вредности у Пајтону су објекти. Односно, све вредности имају понашање и атрибуте. Оне се понашају као вредности које представљају.
Објекти секвенци¶
Инстанце примитивних уграђених вредности попут бројева су непроменљиве. Саме вредности се не могу мењати током извршења програма. Низови, са друге стране, су променљиви.
Променљиви објекти се користе за представљање вредности које се мењају током времена. Нека особа је иста особа од једног до другог дана и поред тога што је остарила, променила фризуру или се изменила на неки други начин. Слично томе, објекат може имати својства која се мењају услед операције мутирања. На пример, могуће је променити садржај низа. Већина промена се врши позивањем метода над објектима низа.
Многе операције измена низова могу се представити кроз пример који илуструје историју карата (додуше драстично поједностављену). Коментари у примерима описују ефекат позива сваке методе.
Карте потичу из древне Кине, највероватније још из деветог века. Рани шпилови су имали само три знака који су одговарали апоенима новца.
>>> кинески = ['новчић', 'ниска', 'мирјада'] # литерал низа
>>> знакови = кинески # два имена односе се на исти низ
Како су карте стигле до Европе (највероватније преко Египта), само се знак новчића задржао у шпанском шпилу (златник).
>>> знакови.pop() # Избаци из низа и врати последњи члан
'мирјада'
>>> знакови.remove('ниска') # Избаци први члан који је једнак аргументу
Додата су још три знака (која су временом еволуирала како у имену тако и у дизајну),
>>> знакови.append('пехар') # Додај члан на крај низа
>>> знакови.extend(['батина', 'мач']) # Додај све чланове низа на крај низа
а Италијани су мачеве звали пикови,
>>> знакови[3] = 'пик' # Замени члан низа
што је дало знакове за традиционални италијански шпил карата.
>>> знакови
['новчић', 'пехар', 'батина', 'пик']
Француска варијанта која се користи и дан данас у Србији мења прва три знака:
>>> знакови[0:3] = ['херц', 'каро', 'треф'] # Замени одрезак низа
>>> знакови
['херц', 'каро', 'треф', 'пик']
Такође постоје методе за уметање, сортирање и изокретање низова. Све ове операције мутације мењају вредност низа, притом не стварајући нови објекат низа.
Манипулација низовима¶
Понашање функција и метода над низовима се може најбоље разумети у смислу мутације и истоветности објеката. Низови имају велики број уграђених метода које су корисне у многим приликама, па је учење и савладавање њиховог понашања корисно за програмерску продуктивност.
Одсецањем низа ствара се нов низ, а почетни низ остаје неизмењен. Одрезак од почетка до краја низа је један од начина да се ископира целокупан садржај низа.
Иако је низ прекопиран, вредности садржане унутар низа нису. Уместо тога, саставља се нов низ који садржи подскуп истих вредности као и одсечен низ. Стога ће промена низа унутар одсеченог низа утицати и на изворни низ.
>>> низА = [11, [12, 13], 14]
>>> низБ = низА[:]
>>> низБ[1][1] = 15
>>> print(низА[1][1])
15
Уграђена функција list ствара нов низ који садржи вредности из аргумента функције, што мора бити итерирајућа вредност као што је секвенца. Поново, вредности које се убацују у новостворени низ се не копирају. Другим речима, позиви list(низ) и низ[:] дају идентичан резултат.
Додавање, односно сабирање два низа ствара нов низ који садржи све вредности првог низа праћене свим вредностима другог низа. Према томе, низА + низБ и низБ + низА у општем случају дају различите вредности за два произвољна низа низА и низБ. Међутим, оператор += се понаша другачије када су низови у питању, а његово понашање је описано у наставку заједно са extend методом.
>>> низА = [[11], 12]
>>> низБ = [13, 14]
>>> низВ = низА + низБ
>>> низГ = низБ + низА
>>> низА[0][0] = 15
>>> низБ[0] = 16
>>> print(низВ)
[[15], 12, 13, 14]
>>> print(низГ)
[13, 14, [15], 12]
Метода append прима једну вредност као свој аргумент и додаје је на крај низа. Аргумент може бити било која вредност, попут броја или пак неког другог низа. Уколико је аргумент методе низ, тада се сам тај низ, а не његова копија, додаје као последњи члан низа. Метода append увек враћа None притом мењајући односно мутирајући низ над којим се позива тако што му повећава дужину за један.
>>> низА = [1, [2, 3]]
>>> низБ = [4, [5, 6]]
>>> број = 7
>>> низА.append(низБ)
>>> низА.append(број)
>>> низБ.append(број)
>>> резултат = низА.append(низА)
>>> print(низА)
[1, [2, 3], [4, [5, 6], 7], 7, [...]]
>>> print(резултат)
None
Метода extend узима итерирајућу вредност као свој аргумент и додаје сваки од чланова на крај низа. Као и append ни ова метода не враћа ништа већ мења, односно мутира изворни низ повећавајући му дужину за дужину итерирајућег аргумента. Наредба x += y за низ x и итерирајућу вредност y је, ако се занемаре неке мање разлике које спадају ван обима овог рукописа, у потпуности еквивалентна наредби x.extend(y). Прослеђивање било ког неитерирајућег аргумента extend методи проузроковаће TypeError грешку.
>>> низА = [1, 2]
>>> низБ = [1, 2]
>>> низВ = [1, 2]
>>> низГ = [3, [4]]
>>> низА.extend(низГ)
>>> низБ += низГ
>>> низВ.append(низГ)
>>> низГ[1][0] = 7
>>> print(низА)
[1, 2, 3, [7]]
>>> print(низБ)
[1, 2, 3, [7]]
>>> print(низВ)
[1, 2, [3, [7]]]
Метода pop уклања и враћа последњи члан низа. Када се методи зада целобројни аргумент i, она уклања и враћа i-ти члан, односно члан са индексом i, из датог низа. У сваком случају, метода мења, односно мутира низ смањујући му дужину за један. Позив pop методе над празним низом резултује IndexError грешком.
>>> x = [0, 1, [2, 3], 4]
>>> y = x.pop(2)
>>> z = x.pop()
>>> print(x)
[0, 1]
>>> print(y)
[2, 3]
>>> print(z)
4
Метода remove прима један аргумент једнак некој вредности која се већ налази унутар низа. Метода уклања први члан у низу који је једнак њеном аргументу. Позив remove методе са вредношћу која се не налази у низу, односно није једнака ниједном члану низа изазива ValueError грешку.
>>> низА = [10, 11, 10, 12, [13, 14]]
>>> низА.remove([13, 14])
>>> низА.remove(10)
>>> print(низА)
[11, 10, 12]
Метода index такође узима један аргумент који мора бити једнак некој вредности унутар низа. Метода враћа индекс првог члана низа чија је вредност једнака њеном аргументу. Позив index методе са вредношћу која није једнака неком члану унутар низа узрокује ValueError грешку.
>>> низА = [13, 14, 13, 12, [13, 14], 15]
>>> низА.index([13, 14])
4
>>> низА.index(13)
0
Метода insert прима два аргумента: индекс и вредност коју треба уметнути. Вредност се затим убацује у низ на месту датог индекса. Сви чланови низа пре задатог индекса остају исти док индекси чланова након њега бивају увећани за један. Ова метода мења, односно мутира низ повећавајући му дужину за један, а затим враћа None вредност.
>>> низА = [0, 1, 2]
>>> низА.insert(0, [3, 4])
>>> низА.insert(2, 5)
>>> низА.insert(5, 6)
>>> низА
[[3, 4], 0, 5, 1, 2, 6]
Метода count позвана с неким чланом низа као својим аргументом враћа колико се пута члан с том вредношћу појављује унутар низа. Уколико пак аргумент није једнак било ком елементу низа, метода count ће вратити вредност 0.
>>> низА = [1, [2, 3], 1, [4, 5]]
>>> низА.count([2, 3])
1
>>> низА.count(1)
2
>>> низА.count(5)
0
Низовна убрајања¶
Низовно убрајање увек ствара нов низ. На пример, модул unicodedata прати званична имена свих знакова у Јуникод алфабету. Могу се потражити знакови који одговарају одређеним именима укључујући, примера ради, и оне за карте.
>>> знаци = ['heart', 'diamond', 'spade', 'club']
>>> from unicodedata import lookup
>>> [lookup('BLACK ' + з.upper() + ' SUIT') for з in знаци]
['♥', '♦', '♠', '♣']
>>> [lookup('WHITE ' + з.upper() + ' SUIT') for з in знаци]
['♡', '♢', '♤', '♧']
Резултујући низови немају заједнички садржај са почетним низом знаци, а вредновање низовног убрајања не мења почетни низ.
Више о Јуникод стандарду за представљање текста може се прочитати у поглављу о Јуникоду интернет књиге Dive Into Python 3.
Поворке¶
Поворка, односно инстанца уграђеног tuple типа податка, је непроменљива секвенца. Поворке се стварају користећи литерал поворке који одваја изразе чланова зарезима. Обле, тј. мале заграде, нису обавезне, али се у пракси често користе. Било који објекти могу бити смештени унутар поворке.
>>> 1, 2 + 3
(1, 5)
>>> ("еци", 1, ("пеци", "пец"))
('еци', 1, ('пеци', 'пец'))
>>> type( (10, 20) )
<class 'tuple'>
Литерали празних и једночланих поворки имају посебну синтаксу.
>>> () # нула чланова - празна поворка
()
>>> (10,) # један члан - једночлана поворка
(10,)
Попут низова, и поворке имају коначну дужину и подржавају избор елемената. Такође поседују и неколико метода које су доступне и за рад са низовима, као што су count и index.
>>> стрелице = ("горе", "горе", "доле", "доле") + ("лево", "десно") * 2
>>> len(стрелице)
8
>>> стрелице[3]
'доле'
>>> стрелице.count("доле")
2
>>> стрелице.index("лево")
4
Међутим, методе за манипулисање садржајем низа нису доступне код поворки из разумљивог разлога јер су поворке непроменљиве.
Иако није могуће променити чланове поворке, могуће је изменити вредност променљивих чланова који се налазе унутар поворке.
>>> гнездо = (10, 20, [30, 40])
>>> гнездо[2].pop()
40
>>> print(гнездо)
(10, 20, [30])
Поворке се имплицитно користе приликом вишеструке доделе вредности. Додела две вредности двема променљивама ствара двочлану поворку, то јест уређени пар, а затим је распакује.
Речници¶
Речници су уграђени Пајтонов тип података за чување и обраду одговарајућих уређених веза. Речник садржи уређене парове кључ-вредност, где су и кључеви и вредности објекти. Сврха речника је да пружи апстракцију за чување и дохватање вредности које се не индексирају узастопним целим бројевима, већ описним кључевима. На тај начин представљају неку врсту уопштених низова, код којих су индекси искључиво цели бројеви.
Ниске обично служе као кључеви, јер су ниске уобичајениа представа имена различитих ствари. Наредни литерал речника даје вредности различитих римских бројева.
>>> римскиБројеви = {'I': 1.0, 'V': 5, 'X': 10}
За претрагу, односно дохватање вредности преко њихових кључева користи се оператор избора члана који је претходно примењиван и на секвенце.
>>> римскиБројеви['X']
10
Речник може имати највише једну вредност за сваки кључ. Додавање нових парова кључ-вредност и промена постојеће вредности кључа може се обавити помоћу наредби доделе.
>>> римскиБројеви['I'] = 1
>>> римскиБројеви['L'] = 50
>>> римскиБројеви
{'I': 1, 'V': 5, 'X': 10, 'L': 50}
Треба приметити у претходном излазу да је 'L' додато на крај речника. Наиме, речници су били неуређена структура података све до Пајтона 3.5. Међутим, почевши од Пајтон верзије 3.6 па надаље, њихов садржај јесте уређен уметањем. Будући да су речници у прошлости били неуређен скупови података, најсигурније је не узимати никакве претпоставке о редоследу којим ће се кључеви и вредности унутар речника чувати и начину на који ће се исписивати и штампати.
Речник као тип података такође подржава различите методе проласка кроз садржај речника у целини. Методе keys, values и items враћају итерирајуће вредности.
>>> sum(римскиБројеви.values())
66
Низ уређених парова кључ-вредност може се претворити у речник позивањем dict уграђене конструкторске функције.
>>> dict([(3, 9), (4, 16), (5, 25)])
{3: 9, 4: 16, 5: 25}
Речници имају нека ограничења:
Кључ речника не може бити или садржати променљиву вредност.
Одређени кључ може бити повезан на највише једну вредност.
Прво ограничење везано је за сам начин имплементације речника у Пајтону. Појединости ове имплемнтације нису предмет и тема овог рукописа. Интуитивно гледано, треба узети у обзир да кључеви говоре Пајтону где да пронађе уређени пар кључ-вредност у меморији рачунара, па ако се кључ промени и сама меморијска локација пара се може изгубити. Поворке се обично користе као кључеви у речницима јер се низови не могу користити пошто су променљиви.
Друго ограничење је последица саме апстракције речника, која је пројектована за чување и дохватање вредности кључева. Вредност за одређени кључ се може пронаћи и дохватити само ако у речнику постоји највише једна таква вредност.
Корисна метода која постоји у речницима јесте get која враћа вредност за одређени кључ ако тај кључ постоји у речнику или, у супротном, неку подразумевану вредност. Аргументи методе get су кључ и подразумевана вредност.
>>> римскиБројеви.get('A', 0)
0
>>> римскиБројеви.get('V', 0)
5
Речници такође имају и синтаксу убрајања аналогну оној у низовима. Израз за кључ и израз за вредност су раздвојени двотачком. Вредновање речничког убрајања ствара нови објекат речника.
>>> {x: x*x for x in range(3,6)}
{3: 9, 4: 16, 5: 25}
Локално стање¶
Низови и речници поседују такозвано локално стање: они мењају вредности које имају одређени садржај у сваком тренутку извршавања програма. Реч „стање” подразумева еволутивни, односно развојни процес у коме се то стање може променити.
Функције такође могу имати и локално стање. На пример, дефинишимо функцију која моделира процес подизања новца са банковног рачуна. Биће направљена функција подигни, која као свој једини аргумент прима износ који треба подићи. Уколико на рачуну има довољно новца да се то подизање изврши, функција подигни ће вратити преостало стање на рачуну након подизања новца. У супоротном, функција подигни ће вратити поруку „Недовољно средстава на рачуну.”.
Имплементација функције подизањеНовца захтева нову врсту наредбе: такозвану nonlocal наредбу. Приликом позива функције подизањеНовца, повезује се променљива стање на неки почетни износ. Затим се дефинише и враћа локална функција подигни која приликом сваког позива најпре ажурира, а затим и враћа вредност променљиве стање.
>>> def подизањеНовца(стање):
... """Враћа функцију подигни која умањује стање рачуна сваким својим позивом."""
... def подигни(износ):
... nonlocal стање # Проглашава променљиву "стање" нелокалном
... if износ > стање:
... return 'Недовољно средстава на рачуну.'
... стање = стање - износ # Пре(по)везује постојећу променљиву стање
... return стање
... return подигни
Наредба nonlocal проглашава да приликом сваке промене везивања променљиве стање, повезивање се мења у првом оквиру у коме је променљива стање већ повезана. Треба се подсетити да би без наредбе nonlocal наредба доделе увек повезала име променљиве у првом оквиру тренутног окружења. Наредба nonlocal указује на то да се име променљиве појављује негде у окружењу ван првог (локалног) оквира или последњег (глобалног) оквира.
Да би функција подигни уопште имала смисла, мора се направити с неким унапред одређеним стањем на рачуну. Функција подизањеНовца је функција вишег реда која прима почетно стање рачуна као аргумент док јој је сама функција подигни повратна вредност.
>>> подигни = подизањеНовца(100)
Сада, примера ради, ако се започне са 100 динара на рачуну, као што је у претходној додели назначено, добија се следећи низ повратних вредности:
>>> подигни(25)
75
>>> подигни(25)
50
>>> подигни(60)
'Недовољно средстава на рачуну.'
>>> подигни(15)
35
У горњем примеру вредновање једног те истог израза подигни(25) даје различите вредности. Према томе, ова кориснички дефинисана функција није чиста. Позивање те функције не само да враћа неку вредност, већ очигледно има и промену саме функције на неки начин као свој бочни ефекат, тако да следећи позив са истим аргументом враћа другачији резултат. Овај бочни ефекат је заправо резултат промене у везивању имена и вредности коју функција подигни врши ван тренутног оквира.
Дијаграмима окружења могуће је илустровати (бочне) ефекте вишеструких позива функцији створеној позивом подизањеНовца.
Прва def наредба се понаша на сасвим уобичајен начин, односно ствара нову користички дефинисану функцију и повезује назив подизањеНовца на ту функцију у глобалном оквиру. Наредни позив функције подизањеНовца ствара и враћа локално дефинисану функцију подигни. Променљива стање је повезана у родитељском оквиру ове функције. Од пресудног значаја је то да постоји само једна веза променљиве стање на неку вредност кроз читав горњи пример.
Даље, вреднује се израз који позива ову функцију, везану на име подигни са износом 25. Тело функције подигни извршава се у новом окружењу које проширује окружење у коме је функцији подигни дефинисана. Праћење ефекта вредновања функције подигни илуструје дејство наредбе nonlocal у Пајтону: променљива изван првог локалног оквира може се мењати наредбом доделе.
Наредба nonlocal мења све преостале наредбе доделе унутар дефиниције функције подигни. Након извршавања nonlocal стање, све наредбе доделе са променљивом стање која се налази на левој страни знака = неће повезати стање у првом оквиру тренутног окружења. Уместо тога, пронаћи ће први оквир у коме је променљива стање већ дефинисана и пре(по)везати име променљиве у том оквиру. За случај да променљива стање није претходно била повезана на неку вредност, наредба nonlocal ће пријавити грешку.
Захваљујући промени повезивања назива стање, промењена је и сама функција подигни. Приликом следећег позива функције, променљива стање имаће вредност 75 уместо 100. Стога, када се функција подигни позове други пут, њена повратна вредност ће бити 50, а не 75. Самим тим, промена у променљивој стање из првог позива функције утиче на резултат другог позива.
Други позив функције подигни, већ по обичају, ствара други локални оквир. Међутим, оба оквира функције подигни имају истог родитеља. Односно, оба проширују окружење подизањеНовца, које садржи повезивање променљиве стање. Отуда, оба оквира деле ту конкретну променљиву и њену везу. Позив функције подигни има као бочни ефекат промену окружења које ће бити проширено будућим позивима функције подигни. Наредба nonlocal омогућава функцији подигни да промени везу, односно вредност променљиве у оквиру функције подизањеНовца.
Од првог сусрета са угнежђеним def наредбама било је приметно да локално дефинисана функција може тражити имена изван својих локалних оквира. Сама nonlocal наредба није потребна да би се приступило нелокалној променљивој. Насупрот томе, само након наредбе nonlocal финкција може да промени вредност променљиве у овим оквирима.
Увођењем nonlocal наредби створена је двострука улога наредби доделе: или мењају локалне везе променљивих или мењају нелокалне везе. У ствари, наредбе доделе су већ имале двоструку улогу: или су стварале нове везе или су превезивале имена већ постојећих променљивих. Додела такође може променити садржај низова и речника. Многобројне улоге додела у Пајтони могу прикрити ефекте извршавања саме наредбе доделе. На програмерима је да јасно документују свој изворни код тако да други могу разумети ефекте додела.
Пајтон подробности¶
Овај узорак нелокалне доделе је општа одлика програмских језика са функцијама вишег реда и лексичком облашћу видљивости. Већина других језика уопште не захтева nonlocal наредбу. Уместо тога, нелокална додела је често подразумевано понашање наредбе доделе.
Пајтон такође има необично ограничење у погледу претраге имена променљивих: унутар тела функције, све инстанце променљиве морају се односити на исти оквир. Као резултат тога, Пајтон не може пронаћи вредност променљиве у нелокалном оквиру, а затим везати ту исту променљиву у локалном оквиру јер би се у том случају истој променљивој приступало у два различита оквира у истој функцији. Ово ограничење омогућава Пајтону да унапред одреди који оквир садржи свако име пре извршавања тела функције. Када се ово ограничење прекрши, долази до збуњујуће поруке о грешци. Да би се ово илустровало практичним примером, функција подизањеНовца се понавља у наставку само без nonlocal наредбе.
>>> def подизањеНовца(стање):
... """Враћа функцију подигни која умањује стање рачуна сваким својим позивом."""
... def подигни(износ):
... if износ > стање:
... return 'Недовољно средстава на рачуну.'
... стање = стање - износ # Пре(по)везује постојећу променљиву стање
... return стање
... return подигни
>>> подигни = подизањеНовца(37)
>>> try:
... подигни(10)
... except UnboundLocalError as грешка:
... print('UnboundLocalError: ' + str(грешка))
UnboundLocalError: local variable 'стање' referenced before assignment
Грешка UnboundLocalError се појављује зато што се променљивој стање локално врши додела, па Пајтон претпоставља да се сва референцирања променљиве стање морају такође појавити у локалном оквиру. Ова грешка се дешава заправо пре но што се сама наредба доделе уопште изврши што имплицира да Пајтон на неки начин разматра ову наредбу и пре њеног извршавања. Када буде излагано пројектовање интерпретатора, биће приказано да су проучавања тела функције пре њеног извршавања прилично честа. У овом случају, Пајтонова пред-обрада је ограничила оквир у коме се променљива стање може појавити и тиме спречила проналажење имена променљиве у окружењу. Додавањем наредбе nonlocal ова грешка се исправља. Иначе, nonlocal наредба није постојала у Пајтону 2.
Предности нелокалне доделе¶
Нелокална додела је важан корак на путу ка посматрању рачунарских програма као скупа независних и аутономних објеката који међусобно дејствују, али сваки од њих управља својим унутрашњим стањем.
Конкретно говорећи, нелокална додела је донела способност да се неко стање које је локално за функцију одржава, али и развија током узастопних позива тој функцији. Променљива стање одређене подигни функције је дељено међу свим позивима те функције. Међутим, вредност повезана с променљивом стање унутар одређене инстанце подигни је недоступна остатку програма. Само је име функције подигни повезано са оквиром функције подизањеНовца унутар кога је дефинисано. Уколико се подизањеНовца поново позове, створиће се нов оквир са засебном променљивом стање.
Горњи пример може се проширити да се и илуструје претходно изнета поента. Други позив функције подизањеНовца враћа другу функцију подигни која има другог родитеља. Ову друга функција се везује за име подигни2 у глобалном оквиру.
>>> def подизањеНовца(стање):
... """Враћа функцију подигни која умањује стање рачуна сваким својим позивом."""
... def подигни(износ):
... nonlocal стање # Проглашава променљиву "стање" нелокалном
... if износ > стање:
... return 'Недовољно средстава на рачуну.'
... стање = стање - износ # Пре(по)везује постојећу променљиву стање
... return стање
... return подигни
>>> подигни1 = подизањеНовца(46)
>>> подигни2 = подизањеНовца(7)
>>> подигни2(6)
1
>>> подигни1(17)
29
Сада се види да заправо постоје две променљиве стање у два различита оквира, а свака подигни функција има другог родитеља. Назив подигни1 везан је на функцију која има променљиву стање с вредношћу 46, док је подигни2 везан за другу функцију с променљивом стање која има вредност 7.
Позив подигни2 мења вредност своје нелокалне променљиве стање, али не утиче на функцију везану на име подигни. Промена променљиве стање од стране функције подигни2 не утиче на будуће позиве функције подигни1 јер је њено стање и даље 46.
На овај начин, свака инстанца функције подигни одржава своје стање променљиве стање, али то стање је недоступно било којој другој функцији у програму. Посматрајући ову ситуацију с вишег нивоа, створена је апстракција банковног рачуна који управља сопственом унутрашњом структуром и појединостима, али се понаша на начин који моделира банковне рачуне у стварном свету, односно рачуне који се временом мењају на основу сопствене историје захтева за подизањем новца.
Цена нелокалне доделе¶
Уведени модел израчунавања унутар окружења се елегантно и чисто проширује како би објаснио ефекте нелокалне доделе. Међутим, нелокална додела носи са собом и неке суптилне нијансе у посматрање и разматрање имена променљивих и вредности.
Све до сада, вредности се нису мењале већ су се само мењали називи (променљивих) и повезивања. Када су два назива (променљивих) а и б била повезана рецимо на вредност 7, није било важно да ли су повезана на исту седмицу или на две различите седмице у меморији. Колико се могло закључити, постојао је само један објекат седмице који се никада није мењао.
Међутим, функције са стањем се не понашају на овај начин. Када су оба назива подигни1 и подигни2 везана на подигни функцију битно је да ли су везана за исту функцију или различите инстанце те функције. Размотримо следећи пример који је другачији од претходних који су управо анализирани. У овом случају, позивање функције назване подигни2 је променило вредност функције назване подигни1 због тога што се оба назива односе на једну те исту функцију.
>>> def подизањеНовца(стање):
... """Враћа функцију подигни која умањује стање рачуна сваким својим позивом."""
... def подигни(износ):
... nonlocal стање # Проглашава променљиву "стање" нелокалном
... if износ > стање:
... return 'Недовољно средстава на рачуну.'
... стање = стање - износ # Пре(по)везује постојећу променљиву стање
... return стање
... return подигни
>>> подигни1 = подизањеНовца(12)
>>> подигни2 = подигни1
>>> подигни2(1)
11
>>> подигни1(1)
10
Није необично да се два назива односе на исту вредност, па је тако и у програмима. Међутим, како се вредности временом мењају, мора се бити веома обазрив како би се разумео ефекат промене на друге називе који би се могли односити на те вредности.
Кључ за исправну и правилну анализу изворног кода који садржи нелокалне доделе јесте да се запамти да само позиви функција могу стварати нове оквире. Наредбе доделе увек мењају повезивање у постојећим оквирима. У претходном случају, осим ако се подизањеНовца не позове два пута, може постојати само једна променљива стање.
Истоветност и промена¶
Ове финесе настају због тога што је, увођењем нечистих функција које мењају нелокално окружење, промењена природа израза. Израз који садржи само чисте позиве функција је референцијално прозиран или референцијално прозрачан, односно његова вредност се не мења ако се један од његових подизраза замени са вредношћу тог подизраза.
Операције пре(по)везивања нарушавају услове референцијалне прозрачности јер поред враћања вредности мењају и окружење. Када се уведе произвољно пре(по)везивање, долази се до трновитог епистемолошког питања: шта значи да две вредности буду исте? У представљеном моделу окружења за израчунавање, две одвојено дефинисане функције нису исте из простог разлога јер се промене једне можда неће одразити на другу.
Уопштено говорећи, све док се објекти података не мењају, може се сматрати да су сложени објекти података ништа друго до спој појединачних делова. На пример, рационални број се у потпуности одређује његовим бројиоцем и имениоцем. Међутим, овај поглед не важи у присуству промена, када сложени објекти података поседује свој „идентитет” који је различит од делова од којих је састављен. Банковни рачун је и даље „исти” банковни рачун чак и ако се промени његово стање кроз подизање новца, и обратно, могу постојати два банковна рачуна која имају исто стање, али су различити објекти.
Упркос компликацијама које несумњиво носи са собом, нелокална додела је моћно средство за писање модуларних програма. Различити делови програма који одговарају различитим оквирима окружења могу се развијати одвојено током извршења програма. Штавише, користећи функције са локалним стањем даје могућност имплементације променљивих типова података. Заправо, могу се имплементирати и реализовати апстрактни типови података који су еквивалентни уграђеним типовима низа list и речника dict који су малочас представљени.
Имплементација низова и речника¶
Програмски језик Пајтон не даје приступ имплементацији низова, већ само апстракцији секвенце и методама за мутирање уграђеним у сам језик. Да би се разумело како би променљиви низови могли бити представљени помоћу функција са локалним стањем, у наставку ће бити развијена имплементација променљиве уланчане листе.
Променљива уланчана листа биће представљена помоћу функције која има уланчану листу као своје локално стање. Листе морају имати својствен идентитет, као и свака друга променљива вредност. Конкретно, за представљање празне променљиве листе није могуће користити None јер две празне листе нису идентичне вредности (на пример, додавање члана једној не додаје тај члан и другој листи), али None is None односно јединствени објекат. С друге стране, две различите функције од којих свака понаособ има празно као своје локално стање биће довољне за разликовање две празне листе.
Уколико је променљива уланчана листа заправо функција, које аргументе она прима? Одговор излаже општи образац у програмирању: функција је диспечерска функција, а њени аргументи су порука праћена додатним аргументима за параметризацију те методе. Ова порука је ниска која именује шта функција треба да ради. Диспечерске функције су у ствари више функција у једној: порука одређује понашање и начин рада функције, а додатни аргументи се користе унутар тог рада.
Променљива уланчана листа из наставка одговара на пет различитих порука: len, getitem, push, pop и str. Прве две имплементирају понашања из апстракције секвенце. Следећа два додају и уклањају први члан листе. Завршна порука враћа представу целокупне уланчане листе у облику ниске.
>>> def променљиваУланчанаЛиста():
... """Враћа функционалну имплементацију променљиве уланчане листе."""
... садржај = празно
... def dispatch(порука, вредност=None):
... nonlocal садржај
... if порука == 'len':
... return дужинаУланчанеЛисте(садржај)
... elif порука == 'getitem':
... return вратиЧланУланчанеЛисте(садржај, вредност)
... elif порука == 'push_first':
... садржај = уланчанаЛиста(вредност, садржај)
... elif порука == 'pop_first':
... f = први(садржај)
... садржај = остатак(садржај)
... return f
... elif порука == 'str':
... return спојУланчануЛисту(садржај, ", ")
... return dispatch
Помоћне функције из претходног поглавља поновљене су у наставку ради комплетности.
>>> празно = 'празно'
>>> def даЛиЈеУланчанаЛиста(с):
... """с је уланчана листа ако је празна или (први, остатак) пар."""
... return с == празно or (len(с) == 2 and даЛиЈеУланчанаЛиста(с[1]))
>>> def уланчанаЛиста(први, остатак):
... """Направи уланчану листу од првог члана и остатка."""
... assert даЛиЈеУланчанаЛиста(остатак), "остатак мора бити уланчана листа."
... return [први, остатак]
>>> def први(с):
... """Враћа први члан уланчане листе с."""
... assert даЛиЈеУланчанаЛиста(с), "први је применљив само на уланчане листе."
... assert с != празно, "празна уланчана листа нема први члан."
... return с[0]
>>> def остатак(с):
... """Враћа остатак чланова уланчане листе с."""
... assert даЛиЈеУланчанаЛиста(с), "остатак је применљив само на уланчане листе."
... assert с != празно, "празна уланчана листа нема остатак."
... return с[1]
>>> def дужинаУланчанеЛисте(с):
... """Враћа дужину уланчане листе с."""
... дужина = 0
... while с != празно:
... с, дужина = остатак(с), дужина + 1
... return дужина
>>> def вратиЧланУланчанеЛисте(с, и):
... """Враћа члан под индексом и уланчане листе с."""
... while и > 0:
... с, и = остатак(с), и - 1
... return први(с)
>>> def спојУланчануЛисту(с, раздвојник):
... """Враћа ниску свих чланова уланчане листе с раздвојених раздвојник-ом."""
... if с == празно:
... return ""
... elif остатак(с) == празно:
... return str(први(с))
... else:
... return str(први(с)) + раздвојник + спојУланчануЛисту(остатак(с), раздвојник)
Такође, може се написати прикладна функција за прављење функционално имплементиране уланчане листе из било које уграђене секвенце једноставним додавањем сваког члана у обрнутом редоследу.
>>> def уПроменљивуУланчануЛисту(извор):
... """Враћа функционалну уланчану листу са истим садржајем као и извор."""
... s = променљиваУланчанаЛиста()
... for element in reversed(извор):
... s('push_first', element)
... return s
У горњој дефиницији, функција reversed прима и враћа итерирајућу вредност. То је још један пример функције која обрађује секвенце.
У овом тренутку могу се направити функционално имплементиране променљиве уланчане листе. Треба имати у виду да је и уланчана листа сама по себи функција.
>>> s = уПроменљивуУланчануЛисту(знакови)
>>> type(s)
<class 'function'>
>>> print(s('str'))
херц, каро, треф, пик
Поред тога, листама могу бити прослеђене поруке које мењају њихов садржај, примера ради за уклањање првог члана листе.
>>> s('pop_first')
'херц'
>>> print(s('str'))
каро, треф, пик
У принципу, операције push_first и pop_first су довољне за произвољне промене листе. Увек је могуће листу потпуно очистити, односно испразнити је избацивањем свих њених чланова, а затим њен претходни садржај заменити жељеним члановима.
Прослеђивање порука¶
Уз мало времена, могу се имплементирати многе корисне операције мутација Пајтонових низова, као што су extend и insert методе. Постоје два начина да се то учини. Први, могле би се имплементирати као функције које користе постојеће поруке pop_first и push_first да би се извршиле неопходне промене. Алтернативно, могле би се додати додатне elif клаузуле у тело диспечера, при чему би свака од њих проверавала нову поруку (нпр., 'extend' или 'insert') и директно примењивала одговарајућу измену садржаја листе.
Овај други приступ, који обухвата логику свих операција над вредностима података у оквиру једне функције која се одазива и реагује на различите поруке јесте програмерска дисциплина под називом прослеђивање порука. Програм који користи прослеђивање порука дефинише диспечерске функције, од којих свака може имати локално стање, и организује израчунавање прослеђивањем „порука” као првог аргумента тим функцијама. Поруке су ниске које одговарају одређеним радњама и понашању функције.
Имплементација речника¶
Могуће је такође имплементирати структуру података налик речнику. У овом случају, биће коришћена листа парова кључ-вредност за чување садржаја речника. Сваки пар је заправо двочлани низ.
>>> def речник():
... """Враћа функционалну имплементацију речника."""
... records = []
... def getitem(key):
... matches = [r for r in records if r[0] == key]
... if len(matches) == 1:
... key, value = matches[0]
... return value
... def setitem(key, value):
... nonlocal records
... non_matches = [r for r in records if r[0] != key]
... records = non_matches + [[key, value]]
... def dispatch(порука, key=None, value=None):
... if порука == 'getitem':
... return getitem(key)
... elif порука == 'setitem':
... setitem(key, value)
... return dispatch
Поново ће за организацију имплементације бити коришћена метода преношења порука. Подржане су две поруке: getitem и setitem. Да би се убацила вредност под одређеним кључем, најпре се филтрирају сви постојећи записи под задатим кључем, а затим се додаје нов. На овај начин се осигурава да се сваки кључ у речнику појављује само једном. Како би се пронашла вредност под одређеним кључем, филтрирају се сви записи који одговарају датом кључу. Сада је могуће користити горњу имплементацију за чување и преузимање вредности.
>>> р = речник()
>>> р('setitem', 3, 9)
>>> р('setitem', 4, 16)
>>> р('getitem', 3)
9
>>> р('getitem', 4)
16
Ова конкретна имплементација речника није оптимизована за брзу претрагу записа јер сваки позив мора филтрирати све записе унутар речника. Пајтонов уграђени тип речника је знатно ефикаснији, али је начин његове имплементације ван оквира овог уџбеника.
Диспечерски речници¶
Диспечерска функција је општа метода за имплементацију сучеља за прослеђивање порука за апстрактне податке. Да би се имплементирало слање поруке до сада је коришћено условно гранање за поређење ниске која садржи поруку са фиксним скупом унапред познатих порука.
Уграђени тип података речник пружа општу методу за тражење вредности под задатим кључем. Уместо коришћења условних гранања за имплементацију диспечера, могу се користити речници са нискама као кључевима.
Променљиви тип података рачун који је дат у наставку имплементиран је као речник. Има свој конструктор рачун и селектор провериСтање, као и функције депонуј и подигни за баратање средствима на рачуну. Штавише, локално стање рачуна се чува у речнику заједно са функцијама које имплементирају његово понашање и све радње.
>>> def рачун(почетноСтање):
... def депонуј(износ):
... диспечер['стање'] += износ
... return диспечер['стање']
... def подигни(износ):
... if износ > диспечер['стање']:
... return 'Insufficient funds'
... диспечер['стање'] -= износ
... return диспечер['стање']
... диспечер = {'депонуј': депонуј,
... 'подигни': подигни,
... 'стање': почетноСтање}
... return диспечер
>>> def подигни(рачун, износ):
... return рачун['подигни'](износ)
>>> def депонуј(рачун, износ):
... return рачун['депонуј'](износ)
>>> def провериСтање(рачун):
... return рачун['стање']
>>> бр = рачун(20)
>>> депонуј(бр, 5)
25
>>> подигни(бр, 17)
8
>>> провериСтање(бр)
8
Назив диспечер унутар тела конструктора рачун је повезан на речник који садржи поруке које рачун прихвата као кључеве. Стање је број, док су поруке депонуј и подигни повезане на функције. Ове функције имају приступ диспечерском речнику диспечер и тако могу читати и мењати стање рачуна. Чувањем стања унутар диспечерског речника, а не директно у оквиру функције рачун избегава се потреба за nonlocal наредбама у депонуј и подигни функцијама.
Оператори += и -= су скраћеница у Пајтону (као и у многим другим програмским језицима) за комбиновано тражење и поновну доделу вредности. Последње две линије кода у наставку су међусобно еквивалентне.
>>> бр = 2
>>> бр = бр + 1
>>> бр += 1
Пропагација ограничења¶
Променљиви подаци дозвољавају симулацију система са променом, али такође омогућавају и изградњу нових врста апстракција. У свеобухватном примеру који следи комбинују се нелокалне доделе, листе и речници како би се изградио систем заснован на ограничењима који подржава израчунавање у више праваца. Изражавање програма као ограничења је врста такозваног декларативног програмирања у којем програмер декларише структуру проблема који треба решити, али се помоћу апстракције издиже изнад појединости како се тачно израчунава резултат и решење проблема.
Рачунарски програми су традиционално организовани као једносмерна израчунавања која изводе операције над унапред наведеним аргументима како би произвели жељене излазе. С друге стране, често је потребно моделирати системе у погледу односа између различитих физичких величина. На пример, у претходном поглављу је разматрана једначина стања идеалног гаса која повезује притисак (p), запремину (v), количину (n) и температуру (t) идеалног гаса преко Болцманове константе (k):
p * v = n * k * t
Таква једначина није једносмерна, односно ако су дате било које четири величине, претходна једначина може се искористити за израчунавање пете. Упркос томе, превођење ове једначине у традиционални програмски језик на рачунару приморава да се одабере једна од величина која ће се израчунавати у зависности од преостале четири. Дакле, функција за израчунавање притиска не може се користити за израчунавање температуре иако прорачун обе величине проистиче из једне те исте једначине.
У овом одељку биће скицирано пројектовање општег модела линеарних односа. Биће најпре дефинисана примитивна ограничења која важе међу величинама, као што је ограничење сабирач(a, b, c) које намеће математички однос a + b = c.
Такође неопходно је дефинисати средство за комбиновање како би се примитивна ограничења могла комбиновати да се изразе сложенији односи. На овај начин, сам програм личи заправо на програмски језик. Ограничења се комбинују изградњом мреже у којој су ограничења спојена конекторима. Конектор је објекат који „држи” вредност и може учествовати у једном или више ограничења.
Примера ради, зна се да је веза између температуре у Фаренхајтима и Целзијусима:
9 * c = 5 * (f - 32)
Ова једначина је сложено ограничење између величина c и f. Такво ограничење може се посматрати као мрежа која се састоји од примитивних сабирач, множач и константа ограничења.
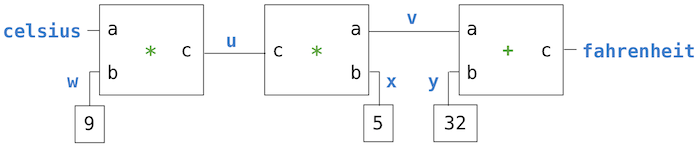
На претходној слици, с леве стране се налази блок за множење са три терминала, означена словима a, b и c. Ови терминали повезују множач са остатком мреже на следећи начин: терминал a је повезан на конектор celsius који садржи температуру у степенима на Целзијусовој скали. Терминал b је повезан на конектор w који је с друге стране повезан на константан блок који садржи 9. Коначно, терминал c који ограничава блок множача да буде производ чинилаца a и b повезан је са терминалом c другог множача, чији је терминал b повезан на константу 5, а терминал a повезан на један од сабирака блока за израчунавање, односно ограничење збира.
Израчунавање путем једне такве мреже одвија се на следећи начин: када конектор добије вредност (од стране корисника или од стране блока за ограничење на који је повезан), он буди сва повезана ограничења (осим блока ограничења који га је управо пробудио) како би их обавестио да има спремну вредност. Сваки пробуђени блок ограничења затим прозива своје конекторе не би ли утврдио да ли има довољно информација за одређивање вредности конектора. Уколико је то случај, блок поставља вредност тог конектора који затим буди све блокове ограничења повезане на њега, и тако даље. На пример, у претварању између Целзијуса и Фаренхајта, w, x и y се константним блоковима одмах постављају на 9, 5 и 32, респективно. Конектори буде множаче и сабирач, који утврђују да нема довољно информација за наставак. За случај да корисник (или неки други део мреже) постави celsius конектор на неку вредност (рецимо 25), пробудиће се крајњи леви множач и поставиће u на вредност \(25 \cdot 9 = 225\). Затим u буди други множач који поставља v на 45, а v буди сабирач, који поставља fahrenheit конектор на 77.
Имплементација система ограничења¶
Као што ће бити приказано, конектори су заправо речници који повезују имена порука на функције и вредности података. Биће имплементирани конектори који одговарају на следеће поруке:
конектор['set_val'](извор, вредност)указује даизворзахтева од конектора да постави своју тренутну вредност навредност.конектор['has_val']()враћа да ли конектор већ има вредност.конектор['val']је тренутна вредност конектора.конектор['forget'](извор)говори конектору даизворзахтева да заборави своју вредност.конектор['connect'](извор)говори конектору да учествује у новом ограничењуизвор.
Ограничења су такође речници који добијају информације од конектора помоћу две различите поруке:
constraint['new_val']()означава да неки конектор који је повезан са ограничењем има нову вредност.constraint['forget']()указује да је неки конектор који је повезан са ограничењем заборавио своју вредност.
Када ограничења приме ове поруке, она их на одговарајући начин шире на друге конекторе.
Функција сабирач ствара ограничење сабирача преко три конектора, при чему је збир прва два једнак трећем: a + b = c. Како би подржао ширење вишесмерног ограничења, сабирач такође мора да ескплицитно наведе да се одузимањем a од c добија b, а да се слично томе одузимањем b од c добија a.
>>> from operator import add, sub
>>> def сабирач(a, b, c):
... """Ограничење да је a + b = c."""
... return тернарноОграничење(a, b, c, add, sub, sub)
У ту сврху, корисно би било имплементирати опште тернарно (тросмерно) ограничење, које користи три конектора и три функције из сабирач-а да би направило ограничење које прихвата поруке new_val и forget. Одговор на поруке су локалне функције које су смештене у речник под именом constraint.
>>> def тернарноОграничење(a, b, c, ab, ca, cb):
... """Ограничење да је ab(a,b)=c и ca(c,a)=b и cb(c,b) = a."""
... def new_value():
... av, bv, cv = [конектор['has_val']() for конектор in (a, b, c)]
... if av and bv:
... c['set_val'](constraint, ab(a['val'], b['val']))
... elif av and cv:
... b['set_val'](constraint, ca(c['val'], a['val']))
... elif bv and cv:
... a['set_val'](constraint, cb(c['val'], b['val']))
... def forget_value():
... for конектор in (a, b, c):
... конектор['forget'](constraint)
... constraint = {'new_val': new_value, 'forget': forget_value}
... for конектор in (a, b, c):
... конектор['connect'](constraint)
... return constraint
Речник под називом constraint је диспечерски речник, али уједно и сам објекат ограничења. Одговара на две поруке које ограничења примају, али се такође прослеђује као аргумент извор у позивима његових конектора.
Локална функција неког ограничења new_value позива се сваки пут када је то ограничење обавештено да један од његових конектора има вредност. Ова функција најпре проверава да ли и a и b имају вредности, па ако је тако говори c конектору да постави своју вредност на повратну вредност функције ab, односно add функцију у случају сабирача. Ограничење прослеђује само себе (constraint) као аргумент извор конектора, који је објекат сабирача. Уколико ни a ни b немају вредности, тада ограничење проверава a и c, и тако редом.
За случај да ограничење буде обавештено да је један од његових конектора заборавио своју вредност оно захтева да сви његови конектори сада забораве своје вредности. (У стварности, губе се само оне вредности које су постављене од стране овог ограничења.)
Ограничење множач је веома слично сабирач-у.
>>> from operator import mul, truediv
>>> def множач(a, b, c):
... """Ограничење да је a * b = c."""
... return тернарноОграничење(a, b, c, mul, truediv, truediv)
Константа је такође ограничење, али оно којем се никада не шаљу никакве поруке јер се састоји из само једног конектора који се поставља на одређену вредност приликом стварања.
>>> def константа(конектор, вредност):
... """Ограничење које је конектор = вредност."""
... constraint = {}
... конектор['set_val'](constraint, вредност)
... return constraint
Ова три ограничења су довољна за имплементацију представљене мреже за претварање температуре.
Представљање конектора¶
Конектор је представљен као речник који садржи вредност, али такође поседује и функције за одговоре са локалним стањем. Конектор мора пратити онога ко му је дао тренутну вредност, такозвани доушник и низ ограничења у којима учествује.
Конструктор конектор има локалне функције за постављање и заборављање вредности, а то су одговори на поруке које долазе из ограничења.
>>> def конектор(име=None):
... """Конектор између ограничења."""
... informant = None
... constraints = []
... def set_value(извор, вредност):
... nonlocal informant
... val = конектор['val']
... if val is None:
... informant, конектор['val'] = извор, вредност
... if име is not None:
... print(име, '=', вредност)
... обавестиСвеОсим(извор, 'new_val', constraints)
... else:
... if val != вредност:
... print('Contradiction detected:', val, 'vs', вредност)
... def forget_value(извор):
... nonlocal informant
... if informant == извор:
... informant, конектор['val'] = None, None
... if име is not None:
... print(име, 'is forgotten')
... обавестиСвеОсим(извор, 'forget', constraints)
... конектор = {'val': None,
... 'set_val': set_value,
... 'forget': forget_value,
... 'has_val': lambda: конектор['val'] is not None,
... 'connect': lambda извор: constraints.append(извор)}
... return конектор
Конектор је поново диспечерски речник за пет порука које ограничења користе за комуникацију са конекторима. Четири одговора су функције, а крајњи одговор је сама вредност.
Локална функција set_value позива се када постоји захтев за постављање вредности конектора. За случај да конектор тренутно нема вредност, поставиће своју вредност и запамтити у променљивој доушник изворно ограничење које је захтевало да се та вредност постави. Тада ће конектор обавестити сва своја повезана ограничења изузев ограничења које је тражило да се поменута вредност постави. Ово се постиже коришћењем следеће итеративне функције.
>>> def обавестиСвеОсим(извор, порука, ограничења):
... """Обавести сва ограничења о поруци порука, изузев извора."""
... for о in ограничења:
... if о != извор:
... о[порука]()
Уколико се од конектора затражи да заборави своју вредност, он позива своју локалну функцију forget_value која најпре проверава да ли захтев долази од истог ограничења које је вредност првобитно поставило и ако је то случај, конектор обавештава повезана ограничења о губитку вредности.
Одговор на has_val поруку указује на то да ли конектор има вредност. Одговор на connect поруку додаје изворно ограничење у низ ограничења.
Коришћење система ограничења¶
Да би се систем ограничења користио за извршавање горе описаних прорачуна температуре, најпре треба направити два именована конектора celsius и fahrenheit позивањем конектор конструктора.
>>> celsius = конектор('Целзијус')
>>> fahrenheit = конектор('Фаренхајт')
Затим се ови конектори повезују у мрежу која одговара претходној шеми. Функција конвертор саставља разне конекторе и ограничења у мрежу.
>>> def конвертор(c, f):
... """Повежи c до f ограничењима да се температура у Целзијусима претвори у Фаренхајте."""
... u, v, w, x, y = [конектор() for _ in range(5)]
... множач(c, w, u)
... множач(v, x, u)
... сабирач(v, y, f)
... константа(w, 9)
... константа(x, 5)
... константа(y, 32)
>>> конвертор(celsius, fahrenheit)
За координацију ограничења и конектора биће коришћен систем за прослеђивање порука. Као што је приказано, ограничења су речници који не садрже сама локална стања. Њихови одговори на поруке су нечисте функције које мењају конекторе које ограничавају.
Конектори су речници који садрже тренутну вредност и одговарају на поруке које манипулишу том вредношћу. Ограничења неће директно мењати вредност конектора, већ ће то учинити слањем порука, тако да као одговор на промену и конектор може да обавести друга ограничења. На овај начин, конектор представља број, али такође обухвата и понашање конектора.
Једна од порука која може бити послата конектору јесте постављање његове вредности. У примеру из наставка, корисник поставља вредност celsius-а на 25.
>>> celsius['set_val']('корисник', 25)
Целзијус = 25
Фаренхајт = 77.0
Не само да се вредност celsius-а мења на 25, већ његова вредност пропагира кроз мрежу и тако мења вредност fahrenheit-а такође. Ове промене су исписане због тога што су ова два конектора именована приликом њиховог стварања.
Сада је могуће покушати да се fahrenheit-у додели нова вредност, рецимо 212.
>>> fahrenheit['set_val']('корисник', 212)
Contradiction detected: 77.0 vs 212
Конектор се жали да је осетио контрадикцију: вредност му је 77.0, а неко покушава да га постави на 212. Уколико се заиста жели да иста мрежа буде поново искоришћена само са новим вредностима, може се рећи celsius-у да заборави своју стару вредност.
>>> celsius['forget']('корисник')
Целзијус is forgotten
Фаренхајт is forgotten
Конектор celsius открива да корисник, који је првобитно поставио његову вредност, сада повлачи ту вредност тако да се celsius слаже да изгуби своју вредност и о томе обавештава остатак мреже. Ове информације се на крају шире све до fahrenheit-а, који сада утврђује да нема разлога да и даље верује да је његова сопствена вредност 77. Дакле, он се такође одриче своје вредности.
Сада када fahrenheit нема вредност, слободно се може поставити на 212:
>>> fahrenheit['set_val']('корисник', 212)
Фаренхајт = 212
Целзијус = 100.0
Ова нова вредност, када се прошири кроз мрежу, присиљава celsius-а да има, односно добије вредност 100. Једна те иста мрежа је коришћена за израчунавање celsius-а задавањем fahrenheit-а, као и за израчунавање fahrenheit-а задавањем celsius-а. Ова неусмереност израчунавања је препознатљива одлика система заснованих на ограничењима.
Програм ограничења који је осмишљен уводи многе идеје које ће се поново појавити у објектно-оријентисаном програмирању. Ограничења и конектори су апстракције којима се манипулише путем порука. Када се вредност конектора промени, она се мења путем поруке која не само да мења вредност, већ је и потврђује (провером извора) и шири даље њене ефекте (обавештавањем других ограничења). У ствари, биће коришћена слична архитектура речника са кључевима који су ниске и вредностима које су заправо функције како би се касније у овом поглављу имплементирао објектно-оријентисани систем.