Рекурзивни објекти¶
Објекти могу имати друге објекте као вредности атрибута. Када објекат неке класе има вредност атрибута исте те класе, то је рекурзивни објекат.
Класа уланчане листе¶
Уланчана листа, представљена раније у овом поглављу, састоји се од првог члана и остатка листе. Остатак повезане листе је сам по себи уланчана листа – рекурзивна дефиниција. Празна листа је посебан случај уланчане листе која нема први члан нити остатак. Уланчана листа је секвенца: има коначну дужину и подржава избор елемената индексом.
Сада се може имплементирати и класа са истим понашањем. У овој верзији биће дефинисано њено понашање користећи посебна имена метода која омогућавају класи да ради са уграђеном функцијом len и оператором избора чланова (углатсе заграде или operator.getitem) у Пајтону. Ове уграђене функције позивају посебна имена класе: дужина се одређује помоћу __len__, а избор чланова обавља се са __getitem__. Празна уланчана листа представљена је празном поворком, која има дужину 0 и нема чланове.
>>> class Листа:
... """Уланчана листа са првим чланом и остатком."""
... празно = ()
... def __init__(self, први, остатак=празно):
... assert остатак is Листа.празно or isinstance(остатак, Листа)
... self.први = први
... self.остатак = остатак
... def __getitem__(self, i):
... if i == 0:
... return self.први
... else:
... return self.остатак[i-1]
... def __len__(self):
... return 1 + len(self.остатак)
>>> с = Листа(3, Листа(4, Листа(5)))
>>> len(с)
3
>>> с[1]
4
Дефиниције за __len__ и __getitem__ су у ствари рекурзивне. Уграђена Пајтон функција len позива методу под називом __len__ када се примени на кориснички дефинисан објекат аргумента. Слично томе, оператор избора члана позива методу под називом __getitem__. Тако ће се унутар тела ове две методе оне саме позивати индиректно. За __len__, основни случај се постиже када се self.остатак вреднује у празну поворку, Листа.празно, која има нулту дужину.
Уграђена функција isinstance враћа да ли први аргумент има тип који јесте или наслеђује други аргумент. Позив isinstance(остатак, Листа) је логички тачан ако је остатак инстанце класе Листа или инстанца неке од поткласа класе Листа.
Ова имплементација је завршена, али инстанцу класе Листа тренутно је тешко прегледати. Да би се припомогло у отклањању грешака, такође се може дефинисати функција претварање објекта класе Листа у текстуални израз, односно у ниску.
>>> def листаИзраз(с):
... """Враћа ниску која би се вредновала у с."""
... if с.остатак is Листа.празно:
... остатак = ''
... else:
... остатак = ', ' + листаИзраз(с.остатак)
... return 'Листа({0}{1})'.format(с.први, остатак)
>>> листаИзраз(с)
'Листа(3, Листа(4, Листа(5)))'
Овај начин приказивања објеката класе Листа је толико згодан да би било добро да се искористи кад год се инстанца класе Листа прикаже. То понашање може се осигурати постављањем функције листаИзраз као вредност за посебан атрибут класе __repr__. Пајтон приказује инстанце кориснички дефинисаних класа позивајући се на њихову __repr__ методу.
>>> Листа.__repr__ = листаИзраз
>>> с
Листа(3, Листа(4, Листа(5)))
Класа Листа поседује својство затворења. Баш као што члан низа и сам може бити низ, тако и Листа може као свој први члан садржати неку другу Листа инстанцу.
>>> сПрва = Листа(с, Листа(6))
>>> сПрва
Листа(Листа(3, Листа(4, Листа(5))), Листа(6))
Уланчана листа сПрва има само два члана, али је њен први члан заправо трочлана уланчана листа.
>>> len(сПрва)
2
>>> len(сПрва[0])
3
>>> сПрва[0][2]
5
Рекурзивне функције су посебно погодне за манипулисање уланчаним листама. На пример, рекурзивна функција прошириЛисту гради ланчану листу која садржи чланове инстанце с класе Листа, плраћене од стране чланова инстанце т класе Листа. Инсталирање ове функције као __add__ методе класе Листа опонаша се понашање уграђеног оператора додавања или конкатенације над уграђеним низовима.
>>> def прошириЛисту(с, т):
... if с is Листа.празно:
... return т
... else:
... return Листа(с.први, прошириЛисту(с.остатак, т))
>>> прошириЛисту(с, с)
Листа(3, Листа(4, Листа(5, Листа(3, Листа(4, Листа(5))))))
>>> Листа.__add__ = прошириЛисту
>>> с + с
Листа(3, Листа(4, Листа(5, Листа(3, Листа(4, Листа(5))))))
Уместо низовних убрајања, једна уланчана листа може се генерисати из друге помоћу две функције вишег реда: mapЛиста и filterЛиста. Доле дефинисана функција mapЛиста примењује функцију f на сваки члан уланчане листе с и израђује уланчану листу која садржи резултате.
>>> def mapЛиста(f, с):
... if с is Листа.празно:
... return с
... else:
... return Листа(f(с.први), mapЛиста(f, с.остатак))
>>> квадрат = lambda x: x*x
>>> mapЛиста(квадрат, с)
Листа(9, Листа(16, Листа(25)))
Функција filterЛиста враћа уланчану листу која садржи све чланове уланчане листе с за које f враћа тачну логичку вредност. Комбинација mapЛиста и filterЛиста може изразити потпуно исту логику као и низовна убрајања.
>>> def filterЛиста(f, с):
... if с is Листа.празно:
... return с
... else:
... filtered = filterЛиста(f, с.остатак)
... if f(с.први):
... return Листа(с.први, filtered)
... else:
... return filtered
>>> непаран = lambda x: x % 2 == 1
>>> mapЛиста(lambda x: x*x, filterЛиста(непаран, с))
Листа(9, Листа(25))
>>> [квадрат(x) for x in [3, 4, 5] if непаран(x)]
[9, 25]
Функција спојЛисту рекурзивно гради ниску која садржи чланове уланчане листе раздвојене раздвајач-ем, односно неким знаком за раздвајање. Резултат је много компактнији текстуални запис од резултата функције листаИзраз.
>>> def спојЛисту(с, раздвајач):
... if с is Листа.празно:
... return ""
... elif с.остатак is Листа.празно:
... return str(с.први)
... else:
... return str(с.први) + раздвајач + спојЛисту(с.остатак, раздвајач)
>>> спојЛисту(с, ", ")
'3, 4, 5'
Рекурзивна изградња¶
Уланчане листе су посебно корисне при постепеној изградњи секвенци, што је ситуација која се често јавља у рекурзивним израчунавањима.
Функција бројПартиција из првог поглавља рачунала је број партиција природног броја \(n\) помоћу делова величине највише \(m\) у поступку преко рекурзивног стабла. Са секвенцама, такође се могу изричито набројати све ове партиције користећи се сличним поступком.
Прати се иста рекурзивна анализа проблема као и током бројања: партиционисање \(n\) коришћењем природних бројева до \(m\) укључује било
партиционисање \(n-m\) помоћу природних бројева \(m\), или
партиционисање \(n\) коришћењем природних бројева до \(m-1\).
За основне случајеве лако се открива да 0 има празну партицију, док је партиционисање негативних бројева или коришћење делова мањих од 1 немогуће.
>>> def партиције(n, m):
... """Враћа уланчану листу партиција броја n користећи се деловима до m.
... Свака партиција је представљена као уланчана лиаста. """
... if n == 0:
... return Листа(Листа.празно) # Листа која садржи празну партицију
... elif n < 0 or m == 0:
... return Листа.празно
... else:
... помоћу_m = партиције(n-m, m)
... са_m = mapЛиста(lambda s: Листа(m, s), помоћу_m)
... без_m = партиције(n, m-1)
... return прошириЛисту(са_m, без_m)
У рекурзивном случају, граде се две подлисте партиција. Прва користи m, па се m додаје сваком члану резултата помоћу_м да се формира са_м.
Резултат партиција је високо угнежђен: уланчана листа уланчаних листа. Користећи спојЛисту са одговарајућим раздвајачима, могу се приказати партиције на начин који је читљив за људе.
>>> def испишиПартиције(n, m):
... листе = партиције(n, m)
... ниске = mapЛиста(lambda s: спојЛисту(s, " + "), листе)
... print(спојЛисту(ниске, "\n"))
>>> испишиПартиције(6, 4)
4 + 2
4 + 1 + 1
3 + 3
3 + 2 + 1
3 + 1 + 1 + 1
2 + 2 + 2
2 + 2 + 1 + 1
2 + 1 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1 + 1
Класа стабла¶
Стабла такође могу бити представљена инстанцама кориснички дефинисаних класа, уместо угнежђеним инстанцама уграђених типова секвенци. Стабло је било која структура података која као атрибут има низ грана које су такође стабла.
Унутрашње вредности¶
Претходно су стабла дефинисана на такав начин да су се све вредности појављивале на листовима стабла. Такође је уобичајено дефинисати стабла која имају унутрашње вредности у корену сваког подстабла. Унутрашња вредност назива се ознака у стаблу. Класа Стабло испод представља таква стабла, у којима свако стабло има секвенцу грана које су уједно и саме стабла.
>>> class Стабло:
... def __init__(self, ознака, гране=()):
... self.ознака = ознака
... for грана in гране:
... assert isinstance(грана, Стабло)
... self.гране = гране
... def __repr__(self):
... if self.гране:
... return 'Стабло({0}, {1})'.format(self.ознака, repr(self.гране))
... else:
... return 'Стабло({0})'.format(repr(self.ознака))
... def is_leaf(self):
... return not self.гране
Класа Стабло може да представља, на пример, вредности израчунате у стаблу израза за рекурзивну имплементацију фиб, функције за израчунавање Фибоначијевог низа бројева. Функција фибСтабло(n) у наставку враћа Стабло које има \(n\)-ти Фибоначијев број као атрибут ознака и траг свих претходно израчунатих Фибоначијевих бројева унутар његових грана.
>>> def фибСтабло(n):
... if n == 1:
... return Стабло(0)
... elif n == 2:
... return Стабло(1)
... else:
... лево = фибСтабло(n-2)
... десно = фибСтабло(n-1)
... return Стабло(лево.ознака + десно.ознака, (лево, десно))
>>> фибСтабло(5)
Стабло(3, (Стабло(1, (Стабло(0), Стабло(1))), Стабло(2, (Стабло(1), Стабло(1, (Стабло(0), Стабло(1)))))))
Овако представљена стабла се такође обрађују помоћу рекурзивних функција. На пример, могу се сумирати ознаке стабла. Као основни случај, повратна вредност празне гране је да нема ознаку.
>>> def збирОзнака(с):
... """Сабира ознаке инстанце Стабла које могу бити и None."""
... return с.ознака + sum([збирОзнака(г) for г in с.гране])
>>> збирОзнака(фибСтабло(5))
10
Такође може се применити мемо, чија имплементација је поновљена из претходног поглавља ради прегледности, за изградњу Фибоначијевог стабла, где се поновљена подстабла само једном стварају у мемоизираној верзији функције фибСтабло, али се више пута користе као гране различитих већих стабала.
>>> def мемо(f):
... кеш = {}
... def мемоизирано(n):
... if n not in кеш:
... кеш[n] = f(n)
... return кеш[n]
... return мемоизирано
>>> фибСтабло = мемо(фибСтабло)
>>> великоФибСтабло = фибСтабло(35)
>>> великоФибСтабло.ознака
5702887
>>> великоФибСтабло.гране[0] is великоФибСтабло.гране[1].гране[1]
True
>>> збирОзнака = мемо(збирОзнака)
>>> збирОзнака(великоФибСтабло)
142587180
Количина рачунарског времена и меморије сачуване памћењем у овим случајевима је огромна. Уместо да се створи 18’454’929 различитих инстанци класе Стабло, сада се ствара само њих 35.
Скупови¶
Поред низова, поворки, и речника, Пајтон има и четврти уграђени тип контејнера који се назива скуп или set. Скуповни литерали следе математичку нотацију чланова затворених у витичастим заградама. Двоструки чланови (дупликати) се уклањају приликом изградње. Скупови су неуређене колекције, па се штампани редослед може разликовати од редоследа чланова у литералу скупа.
>>> с = {3, 2, 1, 4, 4}
>>> с
{1, 2, 3, 4}
Пајтон скупови подржавају разне операције, укључујући и проверу чланства, одређивање дужине и стандардне операције над скуповима као што је пресек и унија
>>> 3 in с
True
>>> len(с)
4
>>> с.union({1, 5})
{1, 2, 3, 4, 5}
>>> с.intersection({6, 5, 4, 3})
{3, 4}
Поред union и intersection, скупови у Пајтону подржавају и неколико других уграђених метода. Предикати isdisjoint, issubset, и issuperset омогућавају поређење скупова. Скупови су променљив тип податка и може им се мењати по један члан помоћу add, remove, discard, и pop. Додатне методе пружају вишечлане мутације, као што су clear и update. Пајтонова документација за скупове у овом тренутку курса требало би да буде довољно разумљива да попуни све појединости.
Имплементација скупова¶
Апстрактно, скуп је збирка различитих објеката који подржавају проверу чланства, унију, пресек и придруживање. Придруживање члана скупу враћа нови скуп који садржи све чланове изворног скупа заједно са новим чланом, ако је различит од свих претходних. Унија и пресек враћају скуп чланова који се појављују у једном од или у оба скупа. Као и код сваке друге апстракције података, на кориснику је потпуна слобода да имплементира било које функције преко било које представе скупова која пружаја ову колекцију понашања.
У остатку овог одељка, разматрају се три начина имплементације скупова који се разликују по својој представи. Ефикасност ових различитих имплементација биће карактерисана анализом величине раста скуповних операција. Биће коришћене класе Листа и Стабло из претходног дела овог одељка, које омогућавају једноставна и елегантна рекурзивна решења за основне операције над скуповима.
Скупови као неуређене секвенце¶
Један од начина представљања скупа је као секвенца у коме се ниједан члан не појављује више од једном. Празан скуп представљен је празном секвенцом. Провера чланства рекурзивно пролази кроз секвенцу.
>>> def празан(с):
... return с is Листа.празно
>>> def скупСадржи(с, в):
... """Враћа True ако и само ако скуп с садржи в."""
... if празан(с):
... return False
... elif с.први == в:
... return True
... else:
... return скупСадржи(с.остатак, в)
>>> с = Листа(4, Листа(1, Листа(5)))
>>> скупСадржи(с, 2)
False
>>> скупСадржи(с, 5)
True
Ова имплементација функције скупСадржи захтева у просеку \(\Theta(n)\) времена за проверу чланства у скупу, где је \(n\) број чланова у скупу, односно величина скупа с. Користећи ову временски линеарну функцију за проверу чланства, може се и придружити члан скупу, такође у линеарном времену.
>>> def придружиСкупу(с, в):
... """Враћа скуп који садржи све чланове скупа с и члан в."""
... if скупСадржи(с, в):
... return с
... else:
... return Листа(в, с)
>>> т = придружиСкупу(с, 2)
>>> т
Листа(2, Листа(4, Листа(1, Листа(5))))
При пројектовању представе, једно од питања које би требало да је од пресудног значаја и којим би се требало позабавити јесте ефикасност. Пресек два скупа скуп1 и скуп2 такође захтева проверу чланства, али овај пут сваки члан из скуп1 мора бити проверен на чланство у скуп2, што доводи до квадратне величине раста броја корака, \(\Theta(n^2)\), за два скупа величине \(n\).
>>> def пресекСкупова(скуп1, скуп2):
... """Враћа скуп који садржи све чланове заједничке за скуп1 и скуп2."""
... return filterЛиста(lambda в: скупСадржи(скуп2, в), скуп1)
>>> пресекСкупова(с, mapЛиста(квадрат, т))
Листа(4, Листа(1))
Када се рачуна унију два скупа, мора се бити на опрезу да се ниједан од чланова не укључи два пута. Функција унијаСкупова такође захтева линеарни број провера чланства, стварајући тако поступак који такође укључује \(\Theta(n^2)\) корака.
>>> def унијаСкупова(скуп1, скуп2):
... """Враћа скуп који садржи све чланове и из скуп1 и из скуп2."""
... скуп1РазликаСкуп2 = filterЛиста(lambda v: not скупСадржи(скуп2, v), скуп1)
... return прошириЛисту(скуп1РазликаСкуп2, скуп2)
>>> унијаСкупова(т, с)
Листа(2, Листа(4, Листа(1, Листа(5))))
Скупови као уређене секвенце¶
Један од начина да се убрзају скуповне операције је промена начина представе тако да се чланови скупа наводе у растућем редоследу. Да би се то учинило неопходан је начин да поређења два објекта како би се могли рећи који је од њих већи. У Пајтону се могу упоређивати многе различите врсте објеката помоћу оператора < и >, али ми ће у овом конкретном примеру акценат бити стављен на бројеве. Биће представљен скуп бројева излиставањем његових чланова у растућем редоследу.
Једна од предности уређивања чланова показује се у функцији скупСадржи: при провери присуства објекта више се не мора пролазити кроз читав скуп. Уколико се дође до члана скупа који је већи од члана који се тражи, већ тада се може закључити да није у скупу:
>>> def скупСадржи(с, в):
... if празан(с) or с.први > в:
... return False
... elif с.први == в:
... return True
... else:
... return скупСадржи(с.остатак, в)
>>> у = Листа(1, Листа(4, Листа(5)))
>>> скупСадржи(у, 0)
False
>>> скупСадржи(у, 4)
True
Колико корака ово штеди? У најгорем случају, ставка која се тражи може бити највећа у скупу, па је број потребних корака исти као и за неуређену представу скупа. С друге стране, ако се претражују ставке, односно чланови различитих величина, може се очекивати да ће се понекад десити да се просто зауставимо одмах у некој тачки при почетку листе, а да ћемо понекад морати да прегледамо већи део листе. У просеку треба очекивати да ће морати да се испита, односно провери око половина чланова у скупу. Тако ће просечан број потребних корака бити око \(\frac{n}{2}\). Ово је и даље \(\Theta(n)\) раст, али у пракси ради нешто брже у просеку у односу на претходну имплементацију.
Упечатљивије убрзање може се постићи поновном имплементацијом функције пресекСкупа. У неуређеној представи, ова операција је захтевала \(\Theta(n^2)\) корака, јер смо извршен потпун пролазак кроз скуп2 за сваки члан из скуп1. Међутим, користећи се уређеном представом, може се упослити и нешто паметнији начин. Наиме, пролази се кроз оба скупа истовремено, пратећи члан ч1 у скуп1 и ч2 у скуп2. Када су ч1 и ч2 једнаки, тај члан се укључује у пресек.
Претпоставити, међутим, да је ч1 мање од ч2. Будући да је ч2 мањи од преосталих чланова из скуп2, може се одмах закључити да се ч1 не може нигде појавити у остатку скуп2 те стога сигурно није у пресеку. Дакле, више није потребно разматрати ч1; он једноставно бива одбачен и прелази се на следећи члан из скуп1. Слична логика напредује кроз чланове из скуп2 када је ч2 < ч1. Ево и саме функције:
>>> def пресекСкупова(скуп1, скуп2):
... if празан(скуп1) or празан(скуп2):
... return Листа.празно
... else:
... ч1, ч2 = скуп1.први, скуп2.први
... if ч1 == ч2:
... return Листа(ч1, пресекСкупова(скуп1.остатак, скуп2.остатак))
... elif ч1 < ч2:
... return пресекСкупова(скуп1.остатак, скуп2)
... elif ч2 < ч1:
... return пресекСкупова(скуп1, скуп2.остатак)
>>> пресекСкупова(у, у.остатак)
Листа(4, Листа(5))
Да би се проценио број корака који је потребан за овај поступак, треба имати на уму да се у сваком кораку смањује величина најмање једног скупа. Стога је потребан број корака највише збир броја чланова из скуп1 и скуп2, а не њихов производ, као што је то био случај код неуређене представе. Ово је раст \(\Theta(n)\), а не \(\Theta(n^2)\) – што представља знатно убрзање, чак и за скупове умерене величине. На пример, пресек два скупа од по сто чланова трајаће око двеста корака, уместо десет хиљада за неуређену представу.
Припајање и унија скупова представљених као уређене секвенце такође се могу израчунати, односно урадити у линеарном времену. Ове имплементације су остављене читаоцима као вежба.
Скупови као бинарна стабла претраге¶
Може се урадити чак и боље од представљања скупова уређеном листом тако што ће се представљени чланови распоредити у облику стабла са тачно две гране. Унос корена стабла садржи један члан скупа. Уноси унутар гране лево укључују све чланове мање од оног у корену. Уноси у грани десно укључују све чланове веће од оног у корену. На доњој слици приказана су нека стабла која представљају скуп {1, 3, 5, 7, 9, 11}. Исти скуп може бити представљен стаблом на више различитих начина. У свим стаблима бинарне претраге, сви чланови у левој грани морају бити мањи од уноса у корену стабла, као што и сви чланови у десном подстаблу морају бити већи од члана који се налази у корену стабла.
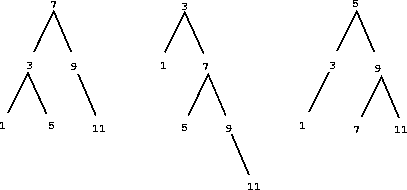
Предност представе преко стабла је следећа: претпоставити да се жели провера да ли се нека вредност в садржи у скупу. Започиње се упоређивањем в и унос. Уколико је в мање, зна се да треба само да се претражи лево подстабло, а ако је в веће, треба само да се претражи десно подстабло. Ако је стабло „уравнотежено”, свако од ових подстабала биће приближно упола мање од почетног. Тако је у само једном кораку сведен проблем претраге стабла величине \(n\) на претрагу стабла величине \(\frac{n}{2}\). Будући да величина стабла бива преполовљена у сваком кораку, требали би очекивати да број корака потребних за претрагу стабла расте као \(\Theta(\log{n})\). За велике скупове ово ће бити значајно убрзање у односу на претходне представе. Ова скупСадржи функција користи структурирано стабло као уређену структуру.
>>> def скупСадржи(с, в):
... if с is None:
... return False
... elif с.унос == в:
... return True
... elif с.унос < в:
... return скупСадржи(с.десно, в)
... elif с.унос > в:
... return скупСадржи(с.лево, в)
Придруживање, односно додавање члана скупу спроводи се на сличан начин и такође захтева \(\Theta(\log{n})\) корака. Да би се додала, то јест придружила вредност в, упоређује се најпре в са унос да би се утврдило да ли в треба додати грани десно или грани лево, а придруживши в одговарајућој грани, саставља се ова новоизграђена грану заједно са оригиналним унос-ом и другом граном . Ако је в једнако унос-у, чвор се само враћа. Уколико се затражи да се в придружи празном стаблу, ствара се Стабло које има в као унос и празне десно и лево гране. Ево и саме функције:
>>> def придружиСкупу(с, в):
... if с is None:
... return Стабло(в)
... elif с.унос == в:
... return с
... elif с.унос < в:
... return Стабло(с.унос, с.лево, придружиСкупу(с.десно, в))
... elif с.унос > в:
... return Стабло(с.унос, придружиСкупу(с.лево, в), с.десно)
Тврдња да се претраживање стабла може извести у логаритамском броју корака почива на претпоставци да је стабло „уравнотежено”, односно да лево и десно подстабло сваког стабла имају приближно једнак број чланова, тако да свако подстабло садржи око половине чланова свог родитеља. Међутим, како се може бити сигуран да ће стабла која се граде бити уравнотежена? Чак и ако се започне са уравнотеженим стаблом, додавање чланова са придружиСкупу може произвести неуравнотежени резултат. Будући да положај новопридруженог члана зависи од тога како се члан упоређује са члановима који су већ у скупу, може се очекивати да ће, ако се чланови додају „случајно”, стабло тежити да буде у просеку уравнотежено.
Међутим ово није гаранција. На пример, ако се започне са празним скупом и редом се придружују бројеви од 1 до 7 у редоследу, на крају ће се добити изузетно неуравнотежено стабло у којем су сва лева подстабла празна, тако да нема предности у односу на једноставну уређену листу. Један од начина за решавање овог проблема је дефинисање операције која претвара произвољно стабло у уравнотежено стабло са истим члановима. Ова трансформација може се извршити након сваких неколико придружиСкупу операција како би се одржала равнотежа скупа.
Операције пресека и уније могу се изводити над скуповима који у основи садрже стабло као структуру у линеарном времену њиховим претварањем у уређене листе и назад. Појединости су остављени као вежба.
Пајтонова имплементација скупова¶
Тип set који је уграђен у Пајтон не користи ниједну од ових представа интерно. Уместо тога, Пајтон користи представу која даје проверу чланства у константном времену и операције придруживања засноване на техници која се назива хеширање, што је тема другог курса. Уграђени Пајтонови скупови не могу садржати променљиве типове података, као што су низови, речници или други скупови. Да би омогућили угнежђени скупови, Пајтон такође укључује уграђену непроменљиву класу frozenset која дели методе са класом set, али искључује методе мутације и операторе.